题目内容
11.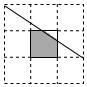 如图,有16个格点,每个格点小正方形的面积为1,给图中间的小正方形内任意投点P,则点P落在图中阴影部分的概率为( )
如图,有16个格点,每个格点小正方形的面积为1,给图中间的小正方形内任意投点P,则点P落在图中阴影部分的概率为( )| A. | $\frac{5}{6}$ | B. | $\frac{7}{8}$ | C. | $\frac{9}{10}$ | D. | $\frac{11}{12}$ |
分析 求出中间正方形中直角三角形的面积,可得阴影部分的面积,即可求出概率.
解答 解:由题意,中间正方形中直角三角形的面积为$\frac{1}{2}$•$\frac{1}{3}$•$\frac{1}{2}$=$\frac{1}{12}$,
∴阴影部分的面积为1-$\frac{1}{12}$=$\frac{11}{12}$,
∴点P落在图中阴影部分的概率是$\frac{11}{12}$,
故选:D.
点评 本题考查几何概率的求法,注意结合概率的性质进行计算求解.用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
19.下列算式中,结果等于x6的是( )
| A. | x2•x2•x2 | B. | x2+x2+x2 | C. | x2•x3 | D. | x4+x2 |
16.下列运算正确的是( )
| A. | 2a+3b=5ab | B. | (-2a2)3=-8a6 | C. | a6÷a2=a3 | D. | ($\frac{1}{2}$)0=0 |
3.下列结论错误的是( )
| A. | 平行四边形既是中心对称又是轴对称图形 | |
| B. | 矩形的四个角相等 | |
| C. | 正方形的对角线互相垂直平分且相等 | |
| D. | 菱形的四条边相等 |
20.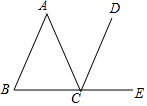 如图,在△ABC中,AB=AC,CD∥AB,点E在BC的延长线上,若∠A=30°,则∠DCE的大小为( )
如图,在△ABC中,AB=AC,CD∥AB,点E在BC的延长线上,若∠A=30°,则∠DCE的大小为( )
 如图,在△ABC中,AB=AC,CD∥AB,点E在BC的延长线上,若∠A=30°,则∠DCE的大小为( )
如图,在△ABC中,AB=AC,CD∥AB,点E在BC的延长线上,若∠A=30°,则∠DCE的大小为( )| A. | 30° | B. | 52.5° | C. | 75° | D. | 85° |
1.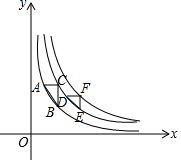 如图,△ABC和△DEF的各顶点分别在双曲线y=$\frac{1}{x}$,y=$\frac{2}{x}$,y=$\frac{3}{x}$在第一象限的图象上,若∠C=∠F=90°,AC∥DF∥x轴,BC∥EF∥y轴,则S△ABC-S△DEF=( )
如图,△ABC和△DEF的各顶点分别在双曲线y=$\frac{1}{x}$,y=$\frac{2}{x}$,y=$\frac{3}{x}$在第一象限的图象上,若∠C=∠F=90°,AC∥DF∥x轴,BC∥EF∥y轴,则S△ABC-S△DEF=( )
 如图,△ABC和△DEF的各顶点分别在双曲线y=$\frac{1}{x}$,y=$\frac{2}{x}$,y=$\frac{3}{x}$在第一象限的图象上,若∠C=∠F=90°,AC∥DF∥x轴,BC∥EF∥y轴,则S△ABC-S△DEF=( )
如图,△ABC和△DEF的各顶点分别在双曲线y=$\frac{1}{x}$,y=$\frac{2}{x}$,y=$\frac{3}{x}$在第一象限的图象上,若∠C=∠F=90°,AC∥DF∥x轴,BC∥EF∥y轴,则S△ABC-S△DEF=( )| A. | $\frac{1}{12}$ | B. | $\frac{1}{6}$ | C. | $\frac{1}{4}$ | D. | $\frac{5}{12}$ |
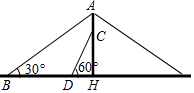 芜湖长江大桥是中国跨度最大的公路和铁路两用桥梁,在同类型重载桥梁中,它的主跨度居世界第二.如图,是该桥面上的一根立柱和拉索的示意图,小明测得拉索AB与水平桥面的夹角是30°,拉索CD与水平桥面的夹角是60°,两拉索底端距离BD为20米,且已知两拉索顶端的距离AC为2米,请求出立柱AH的长.(结果精确到0.1米,$\sqrt{3}$≈1.732)
芜湖长江大桥是中国跨度最大的公路和铁路两用桥梁,在同类型重载桥梁中,它的主跨度居世界第二.如图,是该桥面上的一根立柱和拉索的示意图,小明测得拉索AB与水平桥面的夹角是30°,拉索CD与水平桥面的夹角是60°,两拉索底端距离BD为20米,且已知两拉索顶端的距离AC为2米,请求出立柱AH的长.(结果精确到0.1米,$\sqrt{3}$≈1.732)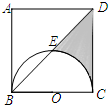 如图,正方形ABCD边长为2,以BC为直径的半圆O交对角线BD于E,则阴影部分面积为(结果保留π)$\frac{3}{2}$-$\frac{π}{4}$.
如图,正方形ABCD边长为2,以BC为直径的半圆O交对角线BD于E,则阴影部分面积为(结果保留π)$\frac{3}{2}$-$\frac{π}{4}$.