题目内容
4.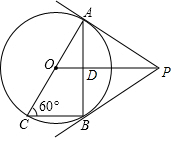 如图,已知AC是⊙O的直径,∠ACB=60°,连结AB,过A、B两点分别作⊙O的切线,两切线交于点P,连接OP交AB于D.
如图,已知AC是⊙O的直径,∠ACB=60°,连结AB,过A、B两点分别作⊙O的切线,两切线交于点P,连接OP交AB于D.(1)求证:OP∥BC;
(2)求证:AD2=OD•DP.
分析 (1)连接OB,根据切线的性质得到PA=PB,∠APO=∠BPO,根据等腰三角形的性质对对对OP垂直平分AB,于是得到结论;
(2)由PA是⊙O的切线,得到∠OAP=90°,根据余角的性质得到∠OAD=∠APD,根据相似三角形的性质即可得到结论.
解答  证明:(1)连接OB,
证明:(1)连接OB,
∵PA,PB是⊙O的切线,
∴PA=PB,∠APO=∠BPO,
∴OP垂直平分AB,
∵AC是⊙O的直径,
∴AB⊥BC,
∴OP∥BC;
(2)∵PA是⊙O的切线,
∴∠OAP=90°,
∴∠ADO=∠ADP=∠OAP=90°,
∴∠OAD+∠PAD=∠PAD+∠APD=90°,
∴∠OAD=∠APD,
∴△OAD∽△DAP,
∴$\frac{AD}{OD}=\frac{OP}{AD}$,
∴AD2=OD•DP.
点评 本题考查了切线的性质,相似三角形的判定和性质,等腰三角形的性质,熟练掌握切线的性质是解题的关键.

练习册系列答案
相关题目
19.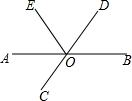 如图,已知直线AB、CD相交于点O,OA平分∠EOC,∠EOC=100°,则∠BOE的大小为( )
如图,已知直线AB、CD相交于点O,OA平分∠EOC,∠EOC=100°,则∠BOE的大小为( )
 如图,已知直线AB、CD相交于点O,OA平分∠EOC,∠EOC=100°,则∠BOE的大小为( )
如图,已知直线AB、CD相交于点O,OA平分∠EOC,∠EOC=100°,则∠BOE的大小为( )| A. | 100° | B. | 110° | C. | 120° | D. | 130° |
9.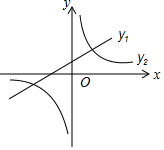 如图,已知一次函数y1=kx+b的图象与反比例函数y2=$\frac{4}{x}$的图象交于(2,m)和(n,-1)两点,观察图象,下列判断正确的是( )
如图,已知一次函数y1=kx+b的图象与反比例函数y2=$\frac{4}{x}$的图象交于(2,m)和(n,-1)两点,观察图象,下列判断正确的是( )
 如图,已知一次函数y1=kx+b的图象与反比例函数y2=$\frac{4}{x}$的图象交于(2,m)和(n,-1)两点,观察图象,下列判断正确的是( )
如图,已知一次函数y1=kx+b的图象与反比例函数y2=$\frac{4}{x}$的图象交于(2,m)和(n,-1)两点,观察图象,下列判断正确的是( )| A. | 当x>2时,y1<y2 | B. | 当x<2时,y1<y2 | C. | 当x>n时,y1<y2 | D. | 当x<n时,y1<y2 |
16.在-2,$\frac{1}{2}$,-3,6四个数中,最小的数是( )
| A. | -2 | B. | $\frac{1}{2}$ | C. | -3 | D. | 6 |
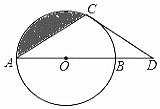 如图,点D在⊙O的直径AB的延长线上,点C在⊙O上,AC=CD,⊙O的半径为3,$\widehat{BC}$的长为π.
如图,点D在⊙O的直径AB的延长线上,点C在⊙O上,AC=CD,⊙O的半径为3,$\widehat{BC}$的长为π.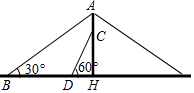 芜湖长江大桥是中国跨度最大的公路和铁路两用桥梁,在同类型重载桥梁中,它的主跨度居世界第二.如图,是该桥面上的一根立柱和拉索的示意图,小明测得拉索AB与水平桥面的夹角是30°,拉索CD与水平桥面的夹角是60°,两拉索底端距离BD为20米,且已知两拉索顶端的距离AC为2米,请求出立柱AH的长.(结果精确到0.1米,$\sqrt{3}$≈1.732)
芜湖长江大桥是中国跨度最大的公路和铁路两用桥梁,在同类型重载桥梁中,它的主跨度居世界第二.如图,是该桥面上的一根立柱和拉索的示意图,小明测得拉索AB与水平桥面的夹角是30°,拉索CD与水平桥面的夹角是60°,两拉索底端距离BD为20米,且已知两拉索顶端的距离AC为2米,请求出立柱AH的长.(结果精确到0.1米,$\sqrt{3}$≈1.732)