题目内容
8.直线y=$\frac{3}{4}$x+b交y轴于A,交x轴于B,将△OAB绕点B旋转至△DCB,A,O的对应点分别是C,D.若BC垂直于x轴,且△ABC的面积是10,点D的坐标是(-$\frac{32}{5}$,-$\frac{16}{5}$)或(-$\frac{8}{5}$,$\frac{16}{5}$)或(-$\frac{8}{5}$,-$\frac{16}{5}$)或(-$\frac{32}{5}$,$\frac{16}{5}$).分析 根据解析式求得A、B的坐标,进而根据三角形的面积求得b的值,即可求得解析式,然后分四种情况分别讨论即可求得.
解答 解:∵直线y=$\frac{3}{4}$x+b交y轴于A,交x轴于B,
∴A(0,b),B(-$\frac{4}{3}$b,0),
∵将△OAB绕点B旋转至△DCB,A,O的对应点分别是C,D.若BC垂直于x轴,△ABC的面积是10,
∴$\frac{1}{2}$×|$\frac{4}{3}$b|•$\sqrt{{b}^{2}+(\frac{4}{3}b)^{2}}$=10,解得b=±3,
①当直线y=$\frac{3}{4}$x+3时,
Ⅰ,如图1:当点C在x轴下方时,作DE⊥x轴于E,
∵∠C+∠DBC=∠EBD+∠CBC=90°,
∴∠C=∠EBD,
∴△BDC∽△DEB,
∴$\frac{DE}{BD}$=$\frac{BE}{DC}$=$\frac{BD}{BC}$,
∵DC=OA=3,BD=OB=4,BC=AB=$\sqrt{O{A}^{2}+O{B}^{2}}$=5,
∴$\frac{DE}{4}$=$\frac{BE}{3}$=$\frac{4}{5}$,
∴DE=$\frac{16}{5}$,BE=$\frac{12}{5}$,
∴OE=4+$\frac{12}{5}$=$\frac{32}{5}$,
∴D(-$\frac{32}{5}$,-$\frac{16}{5}$);
Ⅱ,如图2:当点C在x轴上方时,作DE⊥x轴于E,
∵∠C+∠DBC=∠EBD+∠CBC=90°,
∴∠C=∠EBD,
∴△BDC∽△DEB,
∴$\frac{DE}{BD}$=$\frac{BE}{DC}$=$\frac{BD}{BC}$,
∵DC=3,BD=4,BC=5,
∴$\frac{DE}{4}$=$\frac{BE}{3}$=$\frac{4}{5}$,
∴DE=$\frac{16}{5}$,BE=$\frac{12}{5}$,
∴OE=4-$\frac{12}{5}$=$\frac{8}{5}$,
∴D(-$\frac{8}{5}$,$\frac{16}{5}$);
②当直线y=$\frac{3}{4}$x-3时,
Ⅰ,如图3:当点C在x轴下方时,作DE⊥x轴于E,
同理求得DE=$\frac{16}{5}$,BE=$\frac{12}{5}$,
∴OE=4-$\frac{12}{5}$=$\frac{8}{5}$,
∴D(-$\frac{8}{5}$,-$\frac{16}{5}$);
Ⅱ,如图4:当点C在x轴上方时,作DE⊥x轴于E,
同理证得:DE=$\frac{16}{5}$,BE=$\frac{12}{5}$,
∴OE=4+$\frac{12}{5}$=$\frac{8}{5}$,
∴D(-$\frac{32}{5}$,$\frac{16}{5}$);
综上,点D的坐标为(-$\frac{32}{5}$,-$\frac{16}{5}$)或(-$\frac{8}{5}$,$\frac{16}{5}$)或(-$\frac{8}{5}$,-$\frac{16}{5}$)或(-$\frac{32}{5}$,$\frac{16}{5}$).
故答案为(-$\frac{32}{5}$,-$\frac{16}{5}$)或(-$\frac{8}{5}$,$\frac{16}{5}$)或(-$\frac{8}{5}$,-$\frac{16}{5}$)或(-$\frac{32}{5}$,$\frac{16}{5}$).
点评 本题考查了坐标与图形的变化,以及一次函数图象上的坐标特征,三角形的面积的应用以及三角形相似的判定和性质,分类讨论思想的运用是解题的关键.

 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案| A. | 6,$3\sqrt{2}$ | B. | $3\sqrt{2}$,3 | C. | 6,3 | D. | $6\sqrt{2}$,$3\sqrt{2}$ |
| A. | 1个 | B. | 2个 | C. | 4个 | D. | 3个 |
| A. | 由3x+5=4x得3x-4x=-5 | B. | 由6+x=10得x=10+6 | ||
| C. | 由8x=4-3x得8x-3x=4 | D. | 由2(x-1)=3得2x-1=3 |
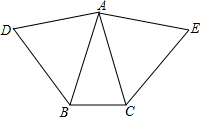 如图所示,△ABC为等腰三角形,分别以它的腰为边作等边三角形ADB和等边三角形ACE,已知∠DAE=∠DBC,求△ABC的三个角的度数(提示:利用方程求解)
如图所示,△ABC为等腰三角形,分别以它的腰为边作等边三角形ADB和等边三角形ACE,已知∠DAE=∠DBC,求△ABC的三个角的度数(提示:利用方程求解)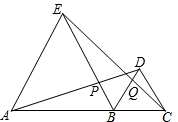 如图,△BDE与△BCD均为等边三角形,连接AD交BE于P,连接CE交BD于Q.
如图,△BDE与△BCD均为等边三角形,连接AD交BE于P,连接CE交BD于Q.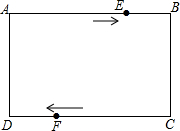 如图,在长方形ABCD中,AB=5cm,AD=3cm.点E从点A出发,以每秒2cm的速度沿折线ABC方向运动,点F从点C出发,以每秒1cm的速度沿线段CD方向向点D运动.已知动点E、F同时发,当点E运动到点C时,E、F停止运动,设运动时间为t.
如图,在长方形ABCD中,AB=5cm,AD=3cm.点E从点A出发,以每秒2cm的速度沿折线ABC方向运动,点F从点C出发,以每秒1cm的速度沿线段CD方向向点D运动.已知动点E、F同时发,当点E运动到点C时,E、F停止运动,设运动时间为t.