题目内容
18.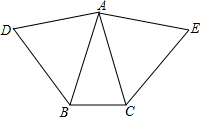 如图所示,△ABC为等腰三角形,分别以它的腰为边作等边三角形ADB和等边三角形ACE,已知∠DAE=∠DBC,求△ABC的三个角的度数(提示:利用方程求解)
如图所示,△ABC为等腰三角形,分别以它的腰为边作等边三角形ADB和等边三角形ACE,已知∠DAE=∠DBC,求△ABC的三个角的度数(提示:利用方程求解)
分析 根据等边三角形各内角为60°,等腰三角形底角相等,三角形内角和为180°、∠DAE=∠DBC即可120°+∠BAC=60°+∠ABC,即可解题.
解答 解:∵AB=AC,
∴∠ABC=∠ACB,故2∠ABC+∠BAC=180°,
∵等边三角形各内角为60°,∠DAE=∠DBC,
∴120°+∠BAC=60°+∠ABC,
又∵2∠ABC+∠BAC=180°,
∴∠BAC=20°.
∴∠ABC=∠ACB=80°,
故△ABC的三个角的度数是80°,80°,20°.
点评 本题考查了等腰三角形底角相等的性质,等边三角形各内角为60°的性质,三角形内角和为180°的性质,本题中求得120°+∠BAC=60°+∠ABC是解题的关键.

练习册系列答案
相关题目
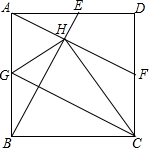 如图,E、F、G分别是正方形ABCD边AD、DC、AB的中点,BE交AF于H点,则下列结论:①BE=AF;②GH=GA;③CB=CH;④AE=2HE.其中结论正确的是( )
如图,E、F、G分别是正方形ABCD边AD、DC、AB的中点,BE交AF于H点,则下列结论:①BE=AF;②GH=GA;③CB=CH;④AE=2HE.其中结论正确的是( ) 已知,在四边形ABCD中,点E为AB上的任一点,过E作EF∥AD交BD于点F,过F作FG∥CD交BC于点G,EG与AC平行吗,为什么?
已知,在四边形ABCD中,点E为AB上的任一点,过E作EF∥AD交BD于点F,过F作FG∥CD交BC于点G,EG与AC平行吗,为什么?