题目内容
3.若正方形的边长为6,则其外接圆半径与内切圆半径的大小分别为( )| A. | 6,$3\sqrt{2}$ | B. | $3\sqrt{2}$,3 | C. | 6,3 | D. | $6\sqrt{2}$,$3\sqrt{2}$ |
分析 由正方形的边长、外接圆半径、内切圆半径正好组成一个直角三角形,从而求得它们的长度.
解答  解:∵正方形的边长为6,
解:∵正方形的边长为6,
∴AB=3,
又∵∠AOB=45°,
∴OB=3
∴AO=$\sqrt{{3}^{2}+{3}^{2}}$=3$\sqrt{2}$,
即外接圆半径为3$\sqrt{2}$,内切圆半径为3.
故选:B.
点评 此题主要考查了正多边形和圆,正确利用正方形的性质得出线段长度是解题关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,点A、C、B、D在同一条直线上,AC=BD,AM∥CN,BM∥DN,那么AM与CN相等吗?请你说明理由.
如图,点A、C、B、D在同一条直线上,AC=BD,AM∥CN,BM∥DN,那么AM与CN相等吗?请你说明理由. 如图,△ABC是等腰直角三角形,点D是BC边的中点,点E,F分别在AC,BC上,连接DE,DF,∠EDF=90°.
如图,△ABC是等腰直角三角形,点D是BC边的中点,点E,F分别在AC,BC上,连接DE,DF,∠EDF=90°.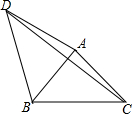 已知:如图,等腰直角△ABC,∠BAC=90°,AB=AC,点D为△ABC外一点,∠ADB=45°,连接CD,AD=4$\sqrt{2}$,CD=10,则四边形ACBD的面积为22.
已知:如图,等腰直角△ABC,∠BAC=90°,AB=AC,点D为△ABC外一点,∠ADB=45°,连接CD,AD=4$\sqrt{2}$,CD=10,则四边形ACBD的面积为22. 如图,点E、F在正方形ABCD的边BC、CD上,BE=CF.
如图,点E、F在正方形ABCD的边BC、CD上,BE=CF.