题目内容
16．已知抛物线y=x2-4与直线y=x+2，求它们的交点坐标．分析 联立两函数解析式，求方程组的解即可求得交点坐标．
解答 解：联立两函数解析式可得$\left\{\begin{array}{l}{y={x}^{2}-4}\\{y=x+2}\end{array}\right.$，
解得$\left\{\begin{array}{l}{x=3}\\{y=5}\end{array}\right.$或$\left\{\begin{array}{l}{x=-2}\\{y=0}\end{array}\right.$，
所以抛物线与直线的交点坐标为（3，5）或（-2，0）．
点评 本题主要考查函数图象的交点，掌握求函数交点坐标的方法是解题的关键，即联立两函数解析式，求方程组的解．
练习册系列答案
相关题目
4．
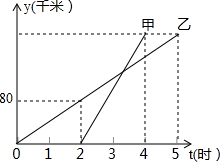甲、乙两车沿相同路线以各自的速度从A地去往B地，如图表示其行驶过程中路程y（千米）随时间t（小时）的变化图象，下列说法：
①乙车比甲车先出发2小时；
②乙车速度为40千米/时；
③A、B两地相距200千米；
④甲车出发80分钟追上乙车．
其中正确的个数为（ ）
甲、乙两车沿相同路线以各自的速度从A地去往B地，如图表示其行驶过程中路程y（千米）随时间t（小时）的变化图象，下列说法：①乙车比甲车先出发2小时；
②乙车速度为40千米/时；
③A、B两地相距200千米；
④甲车出发80分钟追上乙车．
其中正确的个数为（ ）
| A． | 1个 | B． | 2个 | C． | 3个 | D． | 4个 |
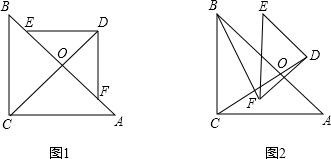
如图，△ABC是等腰直角三角形，点D是BC边的中点，点E，F分别在AC，BC上，连接DE，DF，∠EDF=90°．