题目内容
13.若函数y=x2+ax+b在0≤x≤2上有最小值-$\frac{1}{4}$,最大值2,若-4≤a≤-2,求a,b的值.分析 首先求得抛物线的对称轴,然后根据a的取值范围,确定出1$<-\frac{a}{2}<2$,由抛物线的性质可知当x=-$\frac{a}{2}$时,有最小值,当x=0时,有最大值.
解答 解:抛物线的对称轴为x=$-\frac{a}{2}$,
∵-4≤a≤-2,
∴$1≤-\frac{a}{2}≤2$.
∵函数y=x2+ax+b在0≤x≤2上有最小值-$\frac{1}{4}$,最大值2,
∴当x=-$\frac{a}{2}$时,即$(-\frac{a}{2})^{2}+a(-\frac{a}{2})+b=-\frac{1}{4}$,当x=0时,有最大值,即b=2.
解得:b=2,a1=-3,a2=3(舍去).
∴a=-3,b=2.
点评 本题主要考查的是二次函数的最值问题,找出二次函数的取值最大值和最小值时x的取值是解题的关键.

练习册系列答案
相关题目
3.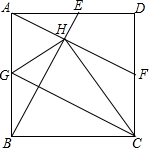 如图,E、F、G分别是正方形ABCD边AD、DC、AB的中点,BE交AF于H点,则下列结论:①BE=AF;②GH=GA;③CB=CH;④AE=2HE.其中结论正确的是( )
如图,E、F、G分别是正方形ABCD边AD、DC、AB的中点,BE交AF于H点,则下列结论:①BE=AF;②GH=GA;③CB=CH;④AE=2HE.其中结论正确的是( )
 如图,E、F、G分别是正方形ABCD边AD、DC、AB的中点,BE交AF于H点,则下列结论:①BE=AF;②GH=GA;③CB=CH;④AE=2HE.其中结论正确的是( )
如图,E、F、G分别是正方形ABCD边AD、DC、AB的中点,BE交AF于H点,则下列结论:①BE=AF;②GH=GA;③CB=CH;④AE=2HE.其中结论正确的是( )| A. | ①②③ | B. | ①②④ | C. | ②③④ | D. | ①②③④ |
4.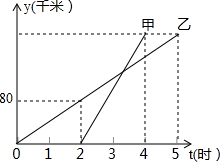 甲、乙两车沿相同路线以各自的速度从A地去往B地,如图表示其行驶过程中路程y(千米)随时间t(小时)的变化图象,下列说法:
甲、乙两车沿相同路线以各自的速度从A地去往B地,如图表示其行驶过程中路程y(千米)随时间t(小时)的变化图象,下列说法:
①乙车比甲车先出发2小时;
②乙车速度为40千米/时;
③A、B两地相距200千米;
④甲车出发80分钟追上乙车.
其中正确的个数为( )
 甲、乙两车沿相同路线以各自的速度从A地去往B地,如图表示其行驶过程中路程y(千米)随时间t(小时)的变化图象,下列说法:
甲、乙两车沿相同路线以各自的速度从A地去往B地,如图表示其行驶过程中路程y(千米)随时间t(小时)的变化图象,下列说法:①乙车比甲车先出发2小时;
②乙车速度为40千米/时;
③A、B两地相距200千米;
④甲车出发80分钟追上乙车.
其中正确的个数为( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
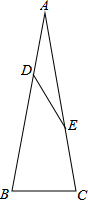 在△ABC中,AB=AC,点D在AB上,点E在AC上,且AD=DE=EC=BC.求证:∠BAC=20°.
在△ABC中,AB=AC,点D在AB上,点E在AC上,且AD=DE=EC=BC.求证:∠BAC=20°.