Question

19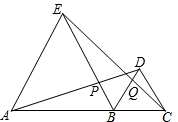．如图，△BDE与△BCD均为等边三角形，连接AD交BE于P，连接CE交BD于Q．
（1）求证：∠DAB=∠BEC；
（2）判断△PQB的形状是直角三角形，等边三角形或等腰三角形或一般三角形中的哪一种？

Answer 1

分析 （1）根据等边三角形的性质就可以证明△BCE≌△BDA，根据全等三角形的对应角相等即可解答；
（2）通过证明△APB≌△EBQ就可以得出BP=BQ，由∠EBQ=60°，就可以得出△PQB是等边三角形．

解答 解：（1）∵△BDE与△BCD均为等边三角形，
∴BE=BA，BD=BC，∠EBA=∠DBC=60°，
∴∠EBA+∠EBD=∠DBC+∠EBD，
∴∠ABD=∠EBC．
在△BCE和△BDA中，
$\left\{\begin{array}{l}{BE=BA}\\{∠ABD=∠EBC}\\{BD=BC}\end{array}\right.$
∴△BCE≌△BDA（SAS），
∴∠DAB=∠BEC；
（2）如图，连接PQ，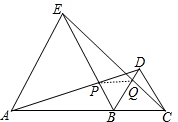

∵△BCE≌△BDA，
∴∠DAB=∠BEC．
∵∠EBA=∠DBC=60°，
∴∠EBQ=60°，
∴∠ABE=∠EBQ．
在△ABD和△EBQ中，
 $\left\{\begin{array}{l}{∠DAB=∠BEC}\\{BA=BE}\\{∠ABE=∠EBQ}\end{array}\right.$，
∴△ABD≌△EBQ（ASA），
∴BP=BQ．
∵∠EBQ=60°，
∴△PQB是等边三角形．

点评 本题考查了等边三角形的性质的运用，三角形的外角与内角的关系的运用，全等三角形的判定与性质的运用，解答时证明三角形全等是解答的关键．