题目内容
17.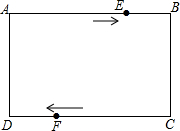 如图,在长方形ABCD中,AB=5cm,AD=3cm.点E从点A出发,以每秒2cm的速度沿折线ABC方向运动,点F从点C出发,以每秒1cm的速度沿线段CD方向向点D运动.已知动点E、F同时发,当点E运动到点C时,E、F停止运动,设运动时间为t.
如图,在长方形ABCD中,AB=5cm,AD=3cm.点E从点A出发,以每秒2cm的速度沿折线ABC方向运动,点F从点C出发,以每秒1cm的速度沿线段CD方向向点D运动.已知动点E、F同时发,当点E运动到点C时,E、F停止运动,设运动时间为t.(1)当E运动到B点时,求出t的值;
(2)在点E、点F的运动过程中,是否存在某一时刻,使得EF=3cm?若存在,请求出t的值;若不存在,请说明理由.
分析 (1)根据题意得出方程2t=5,求出方程的解即可;
(2)画出符合条件的两种情况,根据勾股定理得出方程,求出方程的解即可.
解答 解:(1)∵AB=5cm,
∴2t=5,
解得:t=2.5,
即当E运动到B点时,t的值是2.5秒;
(2)当0<t≤2.5时,如图1,过E作EM⊥DC于,则EM=BC=3cm,
由勾股定理得:(3t-5)+32=32,
解得:t=$\frac{5}{3}$;
当2.5<t≤4时,如图2,
由勾股定理得:(8-2t)2+t2=32,
此方程无解;
即在点E、点F的运动过程中,存在某一时刻,使得EF=3cm,此时t的值是$\frac{5}{3}$秒.
点评 本题考查了矩形的性质,勾股定理的应用,能得出关于t的方程是解此题的关键,注意:矩形的对边相等,矩形的每一个角都是直角.

练习册系列答案
相关题目
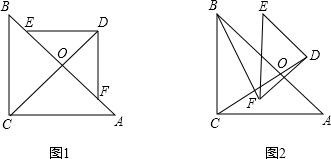
 如图,点E、F在正方形ABCD的边BC、CD上,BE=CF.
如图,点E、F在正方形ABCD的边BC、CD上,BE=CF.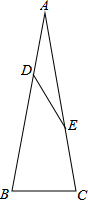 在△ABC中,AB=AC,点D在AB上,点E在AC上,且AD=DE=EC=BC.求证:∠BAC=20°.
在△ABC中,AB=AC,点D在AB上,点E在AC上,且AD=DE=EC=BC.求证:∠BAC=20°.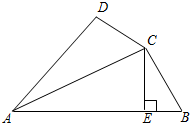 如图,在四边形ABCD中,AC平分∠BAD,CE⊥AB于点E.
如图,在四边形ABCD中,AC平分∠BAD,CE⊥AB于点E.