题目内容
9.现有长为57cm的铁丝,要截成n(n>2)小段,每小段的长度为不小于1cm的整数,如果其中任意3小段都不能拼成三角形,则n的最大值为8.分析 根据三角形的三边关系;三角形两边之和大于第三边,由于每段的长为不小于1的整数,所以设最小的是1,又由于其中任意三段都不能拼成三角形,所以每段长是;1,1,2,3,5,然后依此类推,最后每段的总和要不大于57即可.
解答 解:因为n段之和为定值57cm,故欲n尽可能的大,必须每段的长度尽可能的小.又由于每段的长度不小于1cm,且任意3段都不能拼成三角形,因此这些小段的长度只可能分别是1,1,2,3,5,8,13,21,34,55,
但1+1+2+3+5+8+13+21=54<57,1+1+2+3+5+8+13+21+34=88>57,
所以n的最大值为8.
故答案为8.
点评 此题主要考查了三角形的三边关系,做题时要注意符合题目条件,题目有一定的难度.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
17.如果a>b,那么下列结论中错误的是( )
| A. | a-1>b-1 | B. | 2a>2b | C. | $\frac{a}{3}$$>\frac{b}{3}$ | D. | -4a>-4b |
14.一个多边形截取一个角后,形成另一个多边形的内角和为720°,那么原多边形的边数为( )
| A. | 5 | B. | 5或6 | C. | 5或7 | D. | 5或6或7 |
18.下表中,y是x的一次函数,写出该函数表达式,并补全下表.
| x | -3 | -2 | -1 | 0 | 1 |
| y | 6 | 4 | 2 | 0 | -2 |
 如图,直线AB,CD相交于点O,OA平分∠EOC,若∠EOC:∠EOD=2:3,∠BOD=36度.
如图,直线AB,CD相交于点O,OA平分∠EOC,若∠EOC:∠EOD=2:3,∠BOD=36度.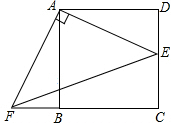 如图,已知点E是正方形ABCD边CD上的一点,点F在CB的延长线上,且DE=BF.求证:△AFE是等腰直角三角形.
如图,已知点E是正方形ABCD边CD上的一点,点F在CB的延长线上,且DE=BF.求证:△AFE是等腰直角三角形.