题目内容
4．
如图，直线AB，CD相交于点O，OA平分∠EOC，若∠EOC：∠EOD=2：3，∠BOD=36度．
分析 根据邻补角的定义求出∠EOC，再根据角平分线的定义求出∠AOC，然后根据对顶角相等解答．
解答 解：∵∠EOC：∠EOD=2：3，
∴∠EOC=180°×$\frac{2}{3+2}$=72°，
∵OA平分∠EOC，
∴∠AOC=$\frac{1}{2}$∠EOC=$\frac{1}{2}$×72°=36°，
∴∠BOD=∠AOC=36°．
故答案为：36．
点评 本题考查了邻补角的定义，对顶角相等的性质，角平分线的定义，是基础题，准确识图是解题的关键．
练习册系列答案
相关题目
15．函数$\frac{1}{2}$≤x≤2时，$\frac{1}{4}$≤y≤1，则这个函数可以是（ ）
| A． | y=$\frac{1}{2x}$ | B． | y=$\frac{2}{x}$ | C． | y=$\frac{1}{8x}$ | D． | y=$\frac{8}{x}$ |
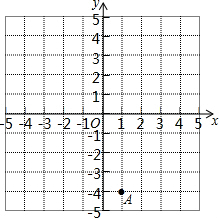如图，在平面直角坐标系内，已知点A的位置；点B的坐标为（3，3）；点C的坐标为（5，1）．
19．
如图，直线m∥n，BA⊥AC于A点，AB、AC分别交直线n于点B、C，∠2=55°，则∠1的度数是（ ）
如图，直线m∥n，BA⊥AC于A点，AB、AC分别交直线n于点B、C，∠2=55°，则∠1的度数是（ ）| A． | 50° | B． | 45° | C． | 35° | D． | 30° |
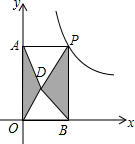如图，点P是反比例函数y=$\frac{6}{x}$（x＞0）的图象上的任意一点，过点P分别作两坐标轴的垂线，与坐标轴构成矩形OAPB，点D是矩形OAPB内任意一点，连接DA、DB、DP、DO，则图中阴影部分的面积是（ ）
如图，AB∥CD，E、F分别在AB、CD上，若∠1+∠D=180°，那么EF与BD平行吗？为什么？