题目内容
1.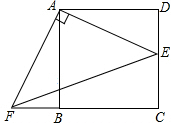 如图,已知点E是正方形ABCD边CD上的一点,点F在CB的延长线上,且DE=BF.求证:△AFE是等腰直角三角形.
如图,已知点E是正方形ABCD边CD上的一点,点F在CB的延长线上,且DE=BF.求证:△AFE是等腰直角三角形.
分析 根据条件可以得出AD=AB,∠ABF=∠ADE=90°,从而可以得出△ABF≌△ADE,就可以得出AF=AE,就可以得出结论.
解答 证明:∵四边形ABCD是正方形,
∴AB=AD,∠ABC=∠D=∠BAD=90°,
∴∠ABF=90°.
∵在△BAF和△DAE中,
$\left\{\begin{array}{l}{AB=AD}\\{∠ABF=∠ADE}\\{BF=DE}\end{array}\right.$,
∴△BAF≌△DAE(SAS),
∴AF=AE,∠FAB=∠EAD,
∵∠EAD+∠BAE=90°,
∴∠FAB+∠BAE=90°,
∴△AEF是等腰直角三角形.
点评 本题考查了正方形的性质的运用,全等三角形的判定及性质的运用,等腰直角三角形的判定,在解答本题时,证明三角形全等是关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
16.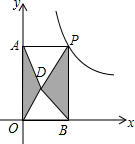 如图,点P是反比例函数y=$\frac{6}{x}$(x>0)的图象上的任意一点,过点P分别作两坐标轴的垂线,与坐标轴构成矩形OAPB,点D是矩形OAPB内任意一点,连接DA、DB、DP、DO,则图中阴影部分的面积是( )
如图,点P是反比例函数y=$\frac{6}{x}$(x>0)的图象上的任意一点,过点P分别作两坐标轴的垂线,与坐标轴构成矩形OAPB,点D是矩形OAPB内任意一点,连接DA、DB、DP、DO,则图中阴影部分的面积是( )
 如图,点P是反比例函数y=$\frac{6}{x}$(x>0)的图象上的任意一点,过点P分别作两坐标轴的垂线,与坐标轴构成矩形OAPB,点D是矩形OAPB内任意一点,连接DA、DB、DP、DO,则图中阴影部分的面积是( )
如图,点P是反比例函数y=$\frac{6}{x}$(x>0)的图象上的任意一点,过点P分别作两坐标轴的垂线,与坐标轴构成矩形OAPB,点D是矩形OAPB内任意一点,连接DA、DB、DP、DO,则图中阴影部分的面积是( )| A. | 1 | B. | 2 | C. | 3 | D. | 4. |
6.下列成语所描述的事件是必然事件的是( )
| A. | 水中捞月 | B. | 水涨船高 | C. | 一箭双雕 | D. | 拔苗助长 |
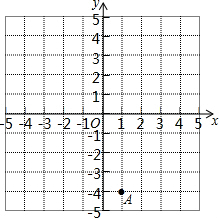 如图,在平面直角坐标系内,已知点A的位置;点B的坐标为(3,3);点C的坐标为(5,1).
如图,在平面直角坐标系内,已知点A的位置;点B的坐标为(3,3);点C的坐标为(5,1). 如图,AB∥CD,E、F分别在AB、CD上,若∠1+∠D=180°,那么EF与BD平行吗?为什么?
如图,AB∥CD,E、F分别在AB、CD上,若∠1+∠D=180°,那么EF与BD平行吗?为什么? 如图,在矩形ABCD中,对角线AC与BD相交于点O,AE垂直且平分线段BO,垂足为点E,BD=15cm,求AC、AB的长.
如图,在矩形ABCD中,对角线AC与BD相交于点O,AE垂直且平分线段BO,垂足为点E,BD=15cm,求AC、AB的长.