题目内容
7.我国《道路交通安全法》第四十七条规定“机动车行经人行横道时,应当减速行驶;遇行人通过人行横道,应当停车让行”.如图:一辆汽车在一个十字路口遇到行人时刹车停下,汽车里的驾驶员看地面的斑马线前后两端的视角分别是∠DCA=30°和∠DCB=60°,如果斑马线的宽度是AB=3米,驾驶员与车头的距离是0.8米,这时汽车车头与斑马线的距离x是多少?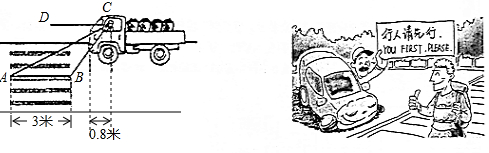
分析 直接利用已知得出∠BAC=∠BCA,则BC=AB,再得出BF的长,求出x的值即可.
解答  解:如图所示:延长AB,
解:如图所示:延长AB,
∵CD∥AB,
∴∠CAB=30°,∠CBF=60°,
∴∠BCA=60°-30°=30°,即∠BAC=∠BCA,
∴BC=AB=3m,
在Rt△BCF中,BC=3m,∠CBF=60°,
∴BF=$\frac{1}{2}$BC=1.5m,
故x=BF-EF=1.5-0.8=0.7(m),
答:这时汽车车头与斑马线的距离x是0.7m.
点评 此题主要考查了含30度角的直角三角形,正确得出BF的长是解题关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
17.下列计算结果错误的是( )
| A. | (ab)7÷(ab)3=(ab)4 | B. | (x2 )3÷(x3 )2=x | ||
| C. | (-$\frac{2}{3}$m)4÷(-$\frac{2}{3}$m)2=(-$\frac{2}{3}$m)2 | D. | (5a)6÷(-5a)4=25a2 |
18. 如图,AB∥CD,下列结论中错误的是( )
如图,AB∥CD,下列结论中错误的是( )
 如图,AB∥CD,下列结论中错误的是( )
如图,AB∥CD,下列结论中错误的是( )| A. | ∠2+∠3=180° | B. | ∠2+∠5=180° | C. | ∠3+∠4=180° | D. | ∠1=∠2 |
12.已知a=411,b=322,c=233,则a、b、c的大小关系为( )
| A. | a>b>c | B. | a>c>b | C. | b>c>a | D. | b>a>c |
 (1)在给定方格纸中画出平移后的△A′B′C′;
(1)在给定方格纸中画出平移后的△A′B′C′;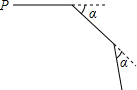 小明从P点出发,沿直线前进10米后向右转a,接着沿直线前进10米,再向右转a,…,照这样走下去,第一次回到出发地点P时,一共走了120米,则a的度数是30°.
小明从P点出发,沿直线前进10米后向右转a,接着沿直线前进10米,再向右转a,…,照这样走下去,第一次回到出发地点P时,一共走了120米,则a的度数是30°. 解不等式(3x+4)(3x-4)-x(x-4)>8(x+1)2,并把它的解集在数轴上表示出来.
解不等式(3x+4)(3x-4)-x(x-4)>8(x+1)2,并把它的解集在数轴上表示出来.