题目内容
1. RT△ABC中,∠C=90°,AC=3,BC=4,A(0,1)
RT△ABC中,∠C=90°,AC=3,BC=4,A(0,1)(1)作出△ABC以A为旋转中心,顺时针旋转90°后所得图形△AB1C1,并写出B1的坐标;
(2)作出△ABC关于原点对称的△A2B2C2,并直接写出B1C1与B2C2的位置关系与大小关系.
分析 (1)利用旋转的性质画出点C、B的对应点C1、B1、从而得到△AB1C1,利用B1C1=BC,AC1=AC可写出B1的坐标;
(2)利用关于原点对称的点的坐标特征写出A2、B2、C2的坐标,然后描点即可得到△A2B2C2,利用旋转的性质判定B1C1与B2C2的位置关系与大小关系.
解答 解:(1)如图,△AB1C1为所作,B1的坐标为(4,4);
(2)如图,△A2B2C2为所作,B1C1与B2C2位置平行且相等.
点评 本题考查了作图-旋转变换:根据旋转的性质可知,对应角都相等都等于旋转角,对应线段也相等,由此可以通过作相等的角,在角的边上截取相等的线段的方法,找到对应点,顺次连接得出旋转后的图形.

练习册系列答案
 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目
11. 已知△ABE≌△ACD,∠A=60°,∠C=25°,则∠BFC的度数为( )
已知△ABE≌△ACD,∠A=60°,∠C=25°,则∠BFC的度数为( )
 已知△ABE≌△ACD,∠A=60°,∠C=25°,则∠BFC的度数为( )
已知△ABE≌△ACD,∠A=60°,∠C=25°,则∠BFC的度数为( )| A. | 70° | B. | 85° | C. | 65° | D. | 以上都不对 |
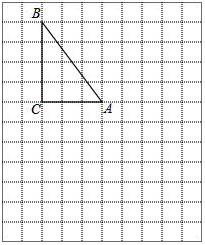 在下列网格图中,每个小正方形的边长均为1个单位,在Rt△ABC中,∠C=90°,AC=3,BC=4.
在下列网格图中,每个小正方形的边长均为1个单位,在Rt△ABC中,∠C=90°,AC=3,BC=4. 如图是二次函数y=ax2+bx+c的图象,下列结论:
如图是二次函数y=ax2+bx+c的图象,下列结论: 李老师用直尺和圆规作已知角的平分线.
李老师用直尺和圆规作已知角的平分线.