题目内容
10. 如图是二次函数y=ax2+bx+c的图象,下列结论:
如图是二次函数y=ax2+bx+c的图象,下列结论:①二次三项式ax2+bx+c的最大值为4;
②4a+2b+c<0;
③一元二次方程ax2+bx+c=1的两根之和为-2;
④使y≤3成立的x的取值范围是x≥0.
其中正确的个数有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 ①求出二次函数的解析式,根据抛物线的顶点坐标确定二次三项式ax2+bx+c的最大值;
②根据x=2时,y<0确定4a+2b+c的符号;
③根据抛物线的对称性确定一元二次方程ax2+bx+c=1的两根之和;
④根据函数图象确定使y≤3成立的x的取值范围.
解答 解:①根据题意得:$\left\{\begin{array}{l}{9a-3b+c=0}&{\;}\\{a+b+c=0}&{\;}\\{c=3}&{\;}\end{array}\right.$,
解得:a=-1,b=-2,c=3,
∴y=-x2-2x+3=-(x+1)2+4,
,∴二次函数图象的顶点坐标为(-1,4),
∴二次三项式ax2+bx+c的最大值为4,故①正确;
②∵当x=2时,y<0,
∴4a+2b+c<0,故②正确;
③∵抛物线与x轴的交点分别是(-3,0),(1,0),
∴一元二次方程ax2+bx+c=0的两根之和=-3+1=-2,故③正确;
④由函数图象可知,当y≤3时,x≥0或x≤-2,故④错误.
故选C.
点评 本题考查的是抛物线与x轴的交点、待定系数法求二次函数的解析式、二次函数图象与系数的关系;由待定系数法求出二次函数的解析式是解答此题的关键.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
20.已知Rt△ABC中,∠C=90°,AC=1,BC=3,则AB的取值范围是( )
| A. | 3.0<AB<3.1 | B. | 3.1<AB<3.2 | C. | 3.2<AB<3.3 | D. | 3.3<AB<3.4 |
 RT△ABC中,∠C=90°,AC=3,BC=4,A(0,1)
RT△ABC中,∠C=90°,AC=3,BC=4,A(0,1) 如图所示,∠A+∠B+∠C+∠D+∠E=180°.
如图所示,∠A+∠B+∠C+∠D+∠E=180°.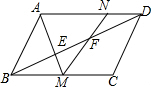 如图,平行四边形ABCD周长为40,∠ABC=60°,E,F在BD上,BE=EF=FD,AE的延长线交BC于M,MF的延长线交AD于N,设BC=x,△ANM的面积为y,求y关于x的函数解析式.
如图,平行四边形ABCD周长为40,∠ABC=60°,E,F在BD上,BE=EF=FD,AE的延长线交BC于M,MF的延长线交AD于N,设BC=x,△ANM的面积为y,求y关于x的函数解析式.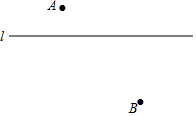 尺规作图(保留作图痕迹):如图,已知直线l及其两侧两点A、B.
尺规作图(保留作图痕迹):如图,已知直线l及其两侧两点A、B.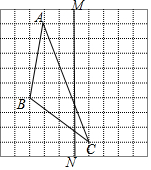 如图,在正方形网格上有一个△ABC.
如图,在正方形网格上有一个△ABC.