题目内容
16.化简$\sqrt{{m}^{2}-4m+4}$+$\sqrt{{m}^{2}+6m+9}$.分析 根据二次根式的加减法则,以及二次根式的性质,化简$\sqrt{{m}^{2}-4m+4}$+$\sqrt{{m}^{2}+6m+9}$即可.
解答 解:$\sqrt{{m}^{2}-4m+4}$+$\sqrt{{m}^{2}+6m+9}$=$\sqrt{{(m-2)}^{2}}$+$\sqrt{{(m+3)}^{2}}$
(1)m<-3时,
原式=2-m-(m+3)=-2m-1.
(2)-3≤m≤2时,
原式=2-m+(m+3)=5.
(3)m>2时,
原式=m-2+(m+3)=2m+1.
点评 此题主要考查了二次根式的加减法,要熟练掌握,解答此题的关键是要明确:二次根式相加减,先把各个二次根式化成最简二次根式,再把被开方数相同的二次根式进行合并,合并方法为系数相加减,根式不变.

练习册系列答案
相关题目
11.下列说法正确的是( )
| A. | 4$\sqrt{3}$-2$\sqrt{3}$=2 | B. | 方程3x2+27=0的解是x=±3 | ||
| C. | 等弧所对的圆周角相等 | D. | 等边三角形是中心对称图形 |
 如图,已知DC是∠ACB的外角平分线,∠BAC与∠1的大小关系如何?∠BAC与∠2呢?∠2与∠B呢?∠BAC与∠B呢?
如图,已知DC是∠ACB的外角平分线,∠BAC与∠1的大小关系如何?∠BAC与∠2呢?∠2与∠B呢?∠BAC与∠B呢?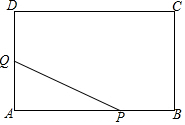 如图,在矩形ABCD中,AB=12cm,BC=9cm.P、Q两点同时从点B、D出发,分别沿BA、DA方向匀速运动(当P运动到A时,P、Q同时停止运动),已知P点的速度比Q点大1cm/s,设P点的运动时间为x秒,△PAQ的面积为ycm2,
如图,在矩形ABCD中,AB=12cm,BC=9cm.P、Q两点同时从点B、D出发,分别沿BA、DA方向匀速运动(当P运动到A时,P、Q同时停止运动),已知P点的速度比Q点大1cm/s,设P点的运动时间为x秒,△PAQ的面积为ycm2, RT△ABC中,∠C=90°,AC=3,BC=4,A(0,1)
RT△ABC中,∠C=90°,AC=3,BC=4,A(0,1)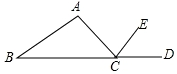 如图,AB=AC,∠A=100°,CE平分∠ACD,求∠ECD的度数.
如图,AB=AC,∠A=100°,CE平分∠ACD,求∠ECD的度数.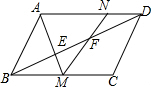 如图,平行四边形ABCD周长为40,∠ABC=60°,E,F在BD上,BE=EF=FD,AE的延长线交BC于M,MF的延长线交AD于N,设BC=x,△ANM的面积为y,求y关于x的函数解析式.
如图,平行四边形ABCD周长为40,∠ABC=60°,E,F在BD上,BE=EF=FD,AE的延长线交BC于M,MF的延长线交AD于N,设BC=x,△ANM的面积为y,求y关于x的函数解析式.