题目内容
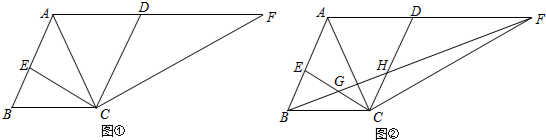
5.如图①,平行四边形ABCD中,AB=AC,CE⊥AB于点E,CF⊥AC交AD的延长线于点F.(1)求证:△BCE∽△AFC;
(2)连接BF,分别交CE、CD于G、H(如图②),求证:EG=CG;
(3)在图②中,若∠ABC=60°,求$\frac{BG}{GF}$.
分析 (1)根据垂直的定义得到∠BEC=∠ACF=90°,由四边形ABCD是平行四边形,得到AB∥CD,根据等腰三角形的性质即可得到结论;
(2)根据相似三角形的性质得到$\frac{BE}{BC}=\frac{AC}{AF}=\frac{AB}{AF}$,根据平行线分线段成比例定理得到$\frac{CH}{BC}=\frac{DH}{DF}=\frac{AB}{AF}$,推出△BGE≌△HGC,根据全等三角形的性质即可得到结论;
(3)根据等边三角形的判定定理得到△ABC是等边三角形,由全等三角形的性质得到BE=CH,等量代换得到CH=DH,于是得到结论.
解答 (1)证明:∵CE⊥AB,CF⊥AC,
∴∠BEC=∠ACF=90°,
∵四边形ABCD是平行四边形,
∴AB∥CD,
又∵AB=AC,∴∠EBC=∠ACB=∠CAF,
∴△BCE∽△AFC;
(2)证明:∵△BCE∽△AFC,
∴$\frac{BE}{BC}=\frac{AC}{AF}=\frac{AB}{AF}$,
∵AD∥BC,AB∥CD,
∴$\frac{CH}{BC}=\frac{DH}{DF}=\frac{AB}{AF}$,
∴BE=CH,
∵AB∥CD,
∴∠BEG=∠HCG,
∠EBG=∠CHG,在△BGE与△HGC中,$\left\{\begin{array}{l}{∠BEG=∠HCG}\\{∠EBG=∠CHG}\\{BE=CH}\\{\;}\end{array}\right.$,
∴△BGE≌△HGC,
∴EG=CG;
(3)解:∵∠ABC=60°,
∴△ABC是等边三角形,
∵CE⊥AB,
∴BE=AE,
∵△BGE≌△HGC,
∴BE=CH,
∴CH=DH,
∵AD∥BC,
∴BH=FH,
∵BG=GH,
∴BG:GF=1:3.
点评 本题考查了全等三角形的判定和性质,相似三角形的判定和性质,等边三角形的判定和性质,平行线的性质,平行线分线段成比例,平行四边形的性质,证得△BGE≌△HGC是解题的关键.

 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案| A. | y=2016x+m | B. | y=$\frac{x}{2{x}^{2}+1}$+$\frac{m}{x}$ | C. | y=x2-2016 | D. | y=$\frac{{x}^{2}}{|x|}$ |
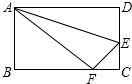 如图,已知矩形ABCD中,AB=8cm,BC=10cm,在边CD上取一点F,将△ADF折叠使点D恰好落在BC边上的点E,则CF的长为4.
如图,已知矩形ABCD中,AB=8cm,BC=10cm,在边CD上取一点F,将△ADF折叠使点D恰好落在BC边上的点E,则CF的长为4.