题目内容
19.已知x-2y=6,x-3y=4,则x2-5xy+6y2的值为24.分析 原式利用十字相乘法分解后,将已知等式代入计算即可求出值.
解答 解:∵x-2y=6,x-3y=4,
∴原式=(x-2y)(x-3y)=24,
故答案为:24.
点评 此题考查了因式分解-十字相乘法,熟练掌握十字相乘法因式分解是解本题的关键.

练习册系列答案
 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案
相关题目
9. 如图,⊙O是△ABC的外接圆,AB是⊙O的直径,I为△ABC的内心,AI的延长线交BC于D,若OI⊥AD,则tan∠CAD的值为( )
如图,⊙O是△ABC的外接圆,AB是⊙O的直径,I为△ABC的内心,AI的延长线交BC于D,若OI⊥AD,则tan∠CAD的值为( )
 如图,⊙O是△ABC的外接圆,AB是⊙O的直径,I为△ABC的内心,AI的延长线交BC于D,若OI⊥AD,则tan∠CAD的值为( )
如图,⊙O是△ABC的外接圆,AB是⊙O的直径,I为△ABC的内心,AI的延长线交BC于D,若OI⊥AD,则tan∠CAD的值为( )| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{\sqrt{5}}{5}$ | D. | $\frac{\sqrt{5}}{2}$ |
7. 如图,正方形ABCD的面积为16,△ABE是等边三角形,点E在正方形ABCD内,在对角线AC上有一点P,使PD+PE的和最小,则这个最小值为( )
如图,正方形ABCD的面积为16,△ABE是等边三角形,点E在正方形ABCD内,在对角线AC上有一点P,使PD+PE的和最小,则这个最小值为( )
 如图,正方形ABCD的面积为16,△ABE是等边三角形,点E在正方形ABCD内,在对角线AC上有一点P,使PD+PE的和最小,则这个最小值为( )
如图,正方形ABCD的面积为16,△ABE是等边三角形,点E在正方形ABCD内,在对角线AC上有一点P,使PD+PE的和最小,则这个最小值为( )| A. | $\sqrt{8}$ | B. | 3 | C. | 4 | D. | $\sqrt{32}$ |
14.若M=2x2-12x+15,N=x2-8x+11,则M与N的大小关系为( )
| A. | M≥N | B. | M>N | C. | M≤N | D. | M<N |
9.如图,∠1与∠2不是同旁内角的是( )
| A. | 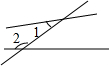 | B. |  | C. | 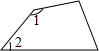 | D. | 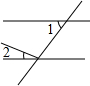 |
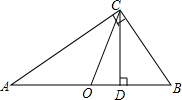 如图,Rt△ABC中,O为斜边中点,CD为斜边上的高.若OC=$\sqrt{6}$,DC=$\sqrt{5}$,则△ABC的面积是$\sqrt{30}$.
如图,Rt△ABC中,O为斜边中点,CD为斜边上的高.若OC=$\sqrt{6}$,DC=$\sqrt{5}$,则△ABC的面积是$\sqrt{30}$.