Question

9．如图，⊙O是△ABC的外接圆，AB是⊙O的直径，I为△ABC的内心，AI的延长线交BC于D，若OI⊥AD，则tan∠CAD的值为（　　）

• A． $\frac{1}{2}$
• B． $\frac{\sqrt{2}}{2}$
• C． $\frac{\sqrt{5}}{5}$
• D． $\frac{\sqrt{5}}{2}$

Answer 1

分析 延长AD交⊙O于E，连接BE，BI，求出∠E=90°，根据内心求出∠3=∠4，∠1=∠2，求出∠3=∠5，∠IBE=∠BIE，推出BE=IE，求出AE=2BE，解直角三角形求出tan∠CAD=tan∠BAE=$\frac{BE}{AE}$，即可求出答案．

解答 解：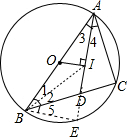
延长AD交⊙O于E，连接BE，BI，
则∠E=90°，
∵I为△ABC的内心，
∴∠3=∠4，∠1=∠2（∠CAD=∠BAE），
∵∠4=∠5，
∴∠3=∠5，
∴∠2+∠5=∠1+∠3，
∴∠IBE=∠BIE，
∴BE=IE，
∵OI⊥AE，OI过O，
∴AE=2AI，
∴AE=2BE，
∴tan∠CAD=tan∠BAE=$\frac{BE}{AE}$=$\frac{BE}{2BE}$=$\frac{1}{2}$．
故选A．

点评 本题考查了三角形的内切圆和内心，三角形的外接圆和外心，垂径定理，圆周角定理，三角形外角性质，等腰三角形的判定等知识点的应用，正确作出辅助线后求出AE=2BE是解此题的关键，有一定的难度．