题目内容
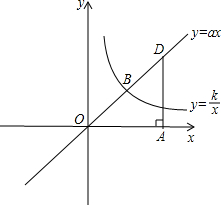 已知正比例函数y=ax与反比例函数y=
已知正比例函数y=ax与反比例函数y=| k |
| x |
(1)求正比例函数和反比例函数的解析式;
(2)延长OB至点D,使得OB=BD,过点D作x轴的垂线,与x轴交于点A,求点A坐标.
考点:反比例函数与一次函数的交点问题
专题:
分析:(1)把点B坐标(2,1)分别代入两函数的解析式,利用待定系数法即可求出答案;
(2)由题意可知点B为OD的中点,由点B坐标为(2,1),根据中点坐标公式可得点D的坐标为(4,2),又DA⊥x轴于点A,从而求得点A坐标为(4,0).
(2)由题意可知点B为OD的中点,由点B坐标为(2,1),根据中点坐标公式可得点D的坐标为(4,2),又DA⊥x轴于点A,从而求得点A坐标为(4,0).
解答:解:(1)∵反比例函数y=
的图象经过点B(2,1),
∴1=
,
∴k=2.
∴反比例函数的表达式为y=
,
∵正比例函数y=ax的图象经过点B(2,1),
∴1=2a,
∴a=
,
∴正比例函数的表达式为y=
x;
(2)∵延长OB至点D,使得OB=BD,
∴B为OD的中点,OD=2OB,
∵点B坐标为(2,1),
∴点D的坐标为(4,2),
∵DA⊥x轴于点A,
∴点A坐标为(4,0).
| k |
| x |
∴1=
| k |
| 2 |
∴k=2.
∴反比例函数的表达式为y=
| 2 |
| x |
∵正比例函数y=ax的图象经过点B(2,1),
∴1=2a,
∴a=
| 1 |
| 2 |
∴正比例函数的表达式为y=
| 1 |
| 2 |
(2)∵延长OB至点D,使得OB=BD,
∴B为OD的中点,OD=2OB,
∵点B坐标为(2,1),
∴点D的坐标为(4,2),
∵DA⊥x轴于点A,
∴点A坐标为(4,0).
点评:本题考查了一次函数和反比例函数的交点问题的应用,利用待定系数法求函数的解析式,中点坐标公式,比较简单.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
在时刻9:30时,时钟上的时针与分针间的夹角是( )
| A、75° | B、90° |
| C、105° | D、120° |
 如图,将两块全等的直角三角形纸片△ABC和△DEF叠放在一起,其中∠C=∠E=90°,AC=DE=12,BC=FE=16,点D是AB的中点,将△DEF绕点D旋转,DE、DF分别交BC于点G、H,使DG=GH,则重叠部分(△DGH)的面积为
如图,将两块全等的直角三角形纸片△ABC和△DEF叠放在一起,其中∠C=∠E=90°,AC=DE=12,BC=FE=16,点D是AB的中点,将△DEF绕点D旋转,DE、DF分别交BC于点G、H,使DG=GH,则重叠部分(△DGH)的面积为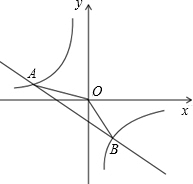 如图,一次函数y=kx+b的图象与反比例函数y=
如图,一次函数y=kx+b的图象与反比例函数y= 如图,要在S区建一个集贸市场,使它到公路、铁路的距离相等,并且离公路与铁路交叉处300米.如果图中1米表示100米,请在图中标出集贸市场的位置.
如图,要在S区建一个集贸市场,使它到公路、铁路的距离相等,并且离公路与铁路交叉处300米.如果图中1米表示100米,请在图中标出集贸市场的位置.