题目内容
某居民小区按照分期付款的方式售房,购房时,首期(第1年)付款50000元,以后每年付款如下表.
(1)根据表格推测,第8年应付款多少元?
(2)如果第x年(其中x>1)应付房款为y元,写出y与x的关系式.
(3)小明家购得一套住房,到第8年恰好付清房款,8年来他家一共交付房款多少元?
| 年份 | 第2年 | 第3年 | 第4年 | 第5年 | 第6年 |
| 交付房款(元) | 15000 | 20000 | 25000 | 30000 | 35000 |
(2)如果第x年(其中x>1)应付房款为y元,写出y与x的关系式.
(3)小明家购得一套住房,到第8年恰好付清房款,8年来他家一共交付房款多少元?
考点:一次函数的应用
专题:
分析:(1)根据表格数据的规律可以得出第7年交付的房款为40000元,第8年交付的房款为45000元;
(2)x>1时,设y与x的关系式为y=kx+b,由待定系数法求出其解即可;
(3)分别求出8年来每年的房款,相加即可.
(2)x>1时,设y与x的关系式为y=kx+b,由待定系数法求出其解即可;
(3)分别求出8年来每年的房款,相加即可.
解答:解:(1)根据图表可发现,每一年增长5000元,得出
第8年应付款45000.
答:第8年应付款45000元;
(2)设应交房款y与年份x的关系式为y=kx+b,由题意,得
,
解得:
.
故第x年(其中x>1)应付房款为y元,的关系式为:y=5000x+5000;
(3)将8年来所有付款求出,相加即可:
30000+15000+20000+25000+30000+35000+40000+45000=240000元.
答:8年来他家一共交付房款240000元.
第8年应付款45000.
答:第8年应付款45000元;
(2)设应交房款y与年份x的关系式为y=kx+b,由题意,得
|
解得:
|
故第x年(其中x>1)应付房款为y元,的关系式为:y=5000x+5000;
(3)将8年来所有付款求出,相加即可:
30000+15000+20000+25000+30000+35000+40000+45000=240000元.
答:8年来他家一共交付房款240000元.
点评:本题主要考查了一次函数的应用以及发现数据的增长规律的运用,待定系数法求一次函数的解析式的运用,解答时求出函数的解析式是解决问题的关键.

练习册系列答案
相关题目
二元一次方程组
的解是( )
|
A、
| |||||
B、
| |||||
C、
| |||||
D、
|
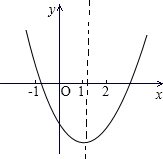 二次函数y=ax2+bx+c的图象如图所示,若M=4a+2b+c,N=a-b+c,P=4a-b,则( )
二次函数y=ax2+bx+c的图象如图所示,若M=4a+2b+c,N=a-b+c,P=4a-b,则( )| A、M>0,N>0,P>0 |
| B、M<0,N>0,P>0 |
| C、M>0,N<0,P>0 |
| D、M<0,N>0,P<0 |
 如图所示的二次函数y=ax2+bx+c的图象中,刘星同学观察得出了下面五条信息:(1)b2-4ac>0;(2)c>1;(3)2a-b<0;(4)a+b+c<0(5)abc>0.你认为其中错误的有( )
如图所示的二次函数y=ax2+bx+c的图象中,刘星同学观察得出了下面五条信息:(1)b2-4ac>0;(2)c>1;(3)2a-b<0;(4)a+b+c<0(5)abc>0.你认为其中错误的有( )| A、1个 | B、2个 | C、3个 | D、4个 |
如图所示的线段或射线,能相交的是( )
A、 |
B、 |
C、 |
D、 |
 如图,AD是∠CAE的平分线,∠B=30°,∠DAE=60°,那么∠ACD等于( )
如图,AD是∠CAE的平分线,∠B=30°,∠DAE=60°,那么∠ACD等于( )| A、90° | B、60° |
| C、80° | D、100° |
 如图,△ABC是以圆锥的左视图,若BC=50,cosB=
如图,△ABC是以圆锥的左视图,若BC=50,cosB=| 5 |
| 12 |
| A、1500π | B、3000π |
| C、750π | D、2000π |
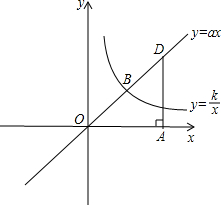 已知正比例函数y=ax与反比例函数y=
已知正比例函数y=ax与反比例函数y=