题目内容
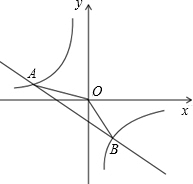 如图,一次函数y=kx+b的图象与反比例函数y=
如图,一次函数y=kx+b的图象与反比例函数y=| n |
| x |
(1)试确定上述反比例函数和一次函数的表达式.
(2)求△AOB的面积.
考点:反比例函数与一次函数的交点问题
专题:
分析:(1)把A点坐标代入反比例函数的解析式,即可求出反比例函数的解析式,再求出B点坐标,把A、B的坐标代入一次函数的解析式,得出方程组,求出方程组的解,即可得出一次函数的解析式;
(2)先求出直线与x轴的交点C的坐标,再根据三角形的面积公式求出三角形AOC和三角形BOC的面积,然后相加即可得出答案.
(2)先求出直线与x轴的交点C的坐标,再根据三角形的面积公式求出三角形AOC和三角形BOC的面积,然后相加即可得出答案.
解答:解:(1)∵点A(-4,2)在反比例函数y=
的图象上,
∴n=(-4)×2=-8,
∴反比例函数的表达式为y=-
,
∵点B(2,m)也在反比例函数y=-
的图象上,
∴m=-4,即B(2,-4),
把点A(-4,2),点B(2,-4)代入一次函数y=kx+b中,
得
,解得
,
 ∴一次函数的表达式为y=-x-2;
∴一次函数的表达式为y=-x-2;
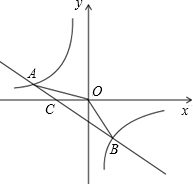
(2)如图,设直线y=-x-2与x轴的交点为C.
∵在y=-x-2中,当y=0时,得x=-2,
∴C(-2,0),
∴△AOB的面积=△AOC的面积+△BOC的面积
=
×2×2+
×2×4
=2+4
=6.
| n |
| x |
∴n=(-4)×2=-8,
∴反比例函数的表达式为y=-
| 8 |
| x |
∵点B(2,m)也在反比例函数y=-
| 8 |
| x |
∴m=-4,即B(2,-4),
把点A(-4,2),点B(2,-4)代入一次函数y=kx+b中,
得
|
|
 ∴一次函数的表达式为y=-x-2;
∴一次函数的表达式为y=-x-2; (2)如图,设直线y=-x-2与x轴的交点为C.
∵在y=-x-2中,当y=0时,得x=-2,
∴C(-2,0),
∴△AOB的面积=△AOC的面积+△BOC的面积
=
| 1 |
| 2 |
| 1 |
| 2 |
=2+4
=6.
点评:本题考查了三角形的面积,用待定系数法求函数的图象,一次函数和反比例函数的交点问题的应用,主要考查学生的计算能力,题目比较好,难度适中.

练习册系列答案
相关题目
在如图所示的四个图中,是正方体的平面展开图的有( )

| A、4个 | B、3个 | C、2个 | D、1个 |
 已知:抛物线C1:y=-
已知:抛物线C1:y=-
| ||
| 3 |
| 3 |
| 5 |
| 3 |
| 3 |
| A、向左平移3个单位 | ||||
| B、向右平移6个单位 | ||||
C、向右平移
| ||||
| D、向左平移6个单位 |
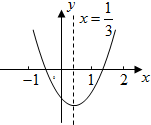 小明从图所示的二次函数y=ax2+bx+c的图象中,观察得出了下面信息:
小明从图所示的二次函数y=ax2+bx+c的图象中,观察得出了下面信息: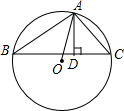 如图,已知△ABC内接于⊙O,AD为BC边上的高.
如图,已知△ABC内接于⊙O,AD为BC边上的高.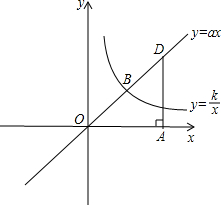 已知正比例函数y=ax与反比例函数y=
已知正比例函数y=ax与反比例函数y= 如图,在每个小正方形的边长均为1个单位长度的方格纸中,有一个△ABC,△ABC的三个顶点均与小正方形的顶点重合.
如图,在每个小正方形的边长均为1个单位长度的方格纸中,有一个△ABC,△ABC的三个顶点均与小正方形的顶点重合.