题目内容
边长为6的正十边形的半径为 .
考点:正多边形和圆
专题:
分析:连接OA、0B,在OB上截取OM=AM,根据正多边形的性质、等腰三角形的性质和判定求出∠AOB=∠MAB,求出△OAB∽△ABM,得出关于R的方程,求出方程的解即可.
解答:解:设AB是圆内接正十边形的一条边,
则AB=6,
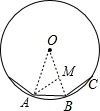 连接OA、0B,在OB上截取OM=AM,
连接OA、0B,在OB上截取OM=AM,
∵∠AOB=
=36°,
∴∠OAM=∠AOB=36°,
∵OA=OB,
∴∠OAB=∠OBA=72°,
∴∠MAB=72°-36°=36°,
∴∠AMB=36°+36°=72°,
∴∠B=∠AMB,
∴AB=AM=OM=6,
设AO=OB=R,
即∠B=∠B,∠MAB=∠AOB,
∴△OAB∽△ABM,
∴
=
,
∴
=
,
解得:R=3+3
(负数舍去),
故答案为:3+3
.
则AB=6,
 连接OA、0B,在OB上截取OM=AM,
连接OA、0B,在OB上截取OM=AM,∵∠AOB=
| 360° |
| 10 |
∴∠OAM=∠AOB=36°,
∵OA=OB,
∴∠OAB=∠OBA=72°,
∴∠MAB=72°-36°=36°,
∴∠AMB=36°+36°=72°,
∴∠B=∠AMB,
∴AB=AM=OM=6,
设AO=OB=R,
即∠B=∠B,∠MAB=∠AOB,
∴△OAB∽△ABM,
∴
| AB |
| BM |
| AO |
| AM |
∴
| 6 |
| R-6 |
| R |
| 6 |
解得:R=3+3
| 5 |
故答案为:3+3
| 5 |
点评:本题考查了正多边形和圆,相似三角形的性质和判定,正多边形的性质,等腰三角形的性质和判定的应用,解此题的关键是构造相似三角形,并进一步得出关于R的方程,难度适中.

练习册系列答案
 步步高达标卷系列答案
步步高达标卷系列答案
相关题目
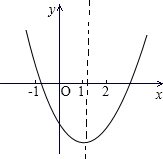 二次函数y=ax2+bx+c的图象如图所示,若M=4a+2b+c,N=a-b+c,P=4a-b,则( )
二次函数y=ax2+bx+c的图象如图所示,若M=4a+2b+c,N=a-b+c,P=4a-b,则( )| A、M>0,N>0,P>0 |
| B、M<0,N>0,P>0 |
| C、M>0,N<0,P>0 |
| D、M<0,N>0,P<0 |
 如图所示的二次函数y=ax2+bx+c的图象中,刘星同学观察得出了下面五条信息:(1)b2-4ac>0;(2)c>1;(3)2a-b<0;(4)a+b+c<0(5)abc>0.你认为其中错误的有( )
如图所示的二次函数y=ax2+bx+c的图象中,刘星同学观察得出了下面五条信息:(1)b2-4ac>0;(2)c>1;(3)2a-b<0;(4)a+b+c<0(5)abc>0.你认为其中错误的有( )| A、1个 | B、2个 | C、3个 | D、4个 |
如图所示的线段或射线,能相交的是( )
A、 |
B、 |
C、 |
D、 |
 如图,⊙O是△ABC的外接圆AC是⊙O的直径,OD⊥BC于点D.OD=2,则AB的长是( )
如图,⊙O是△ABC的外接圆AC是⊙O的直径,OD⊥BC于点D.OD=2,则AB的长是( )| A、1 | B、2 | C、3 | D、4 |
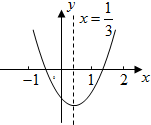 小明从图所示的二次函数y=ax2+bx+c的图象中,观察得出了下面信息:
小明从图所示的二次函数y=ax2+bx+c的图象中,观察得出了下面信息: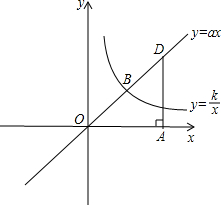 已知正比例函数y=ax与反比例函数y=
已知正比例函数y=ax与反比例函数y=