题目内容
在△ABC中,AB=2
,AC=4,BC=2,以AB为边在△ABC外作△ABD,使△ABD为等腰直角三角形.
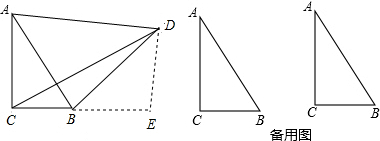
(1)如图,延长CB,过点D作DE⊥CB于点E,请写出图中的一对全等三角形,并求线段CD的长.
(2)以AB为边向外作的等腰直角三角形△ABD还有其他作法吗?如果有,请在备用图中画出图形,并求线段CD的长.
| 5 |

(1)如图,延长CB,过点D作DE⊥CB于点E,请写出图中的一对全等三角形,并求线段CD的长.
(2)以AB为边向外作的等腰直角三角形△ABD还有其他作法吗?如果有,请在备用图中画出图形,并求线段CD的长.
考点:全等三角形的判定与性质,等腰直角三角形
专题:
分析:(1)根据题意中的△ABD为等腰直角三角形,∠ABD=90°,然后巧妙构造辅助线,出现全等三角形和直角三角形,利用全等三角形的性质和勾股定理进行求解.
(2)除去(1)的这种情况,还有两种情况:∠BAD=90°,∠ADB=90°.然后构造辅助线,出现全等三角形和直角三角形,利用全等三角形的性质和勾股定理进行求解.
(2)除去(1)的这种情况,还有两种情况:∠BAD=90°,∠ADB=90°.然后构造辅助线,出现全等三角形和直角三角形,利用全等三角形的性质和勾股定理进行求解.
解答: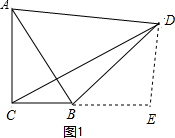 解:(1)如图1,△ACB≌△BED;
解:(1)如图1,△ACB≌△BED;
∵AC=4,BC=2,AB=2
,
∴AC2+BC2=AB2,!
∴△ACB为直角三角形,∠ACB=90°,
延长CB,过点D作DE⊥CB于点E,
∵DE⊥CB,
∴∠BED=∠ACB=90°,
∴∠CAB+∠CBA=90°,
∵△ABD为等腰直角三角形,
∴AB=BD,∠ABD=90°,
∴∠CBA+∠DBE=90°,
∴∠CAB=∠EBD,
在△ACB与△BED中,
,
∴△ACB≌△BED(AAS),
∴BE=AC=4,DE=CB=2,
∴CE=6,
根据勾股定理得:CD=2
;
(2)还有两种,
如图2,过点D作DE⊥CA,垂足为点E.
∵BC⊥CA,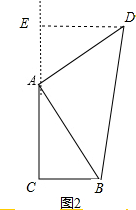
∴∠AED=∠ACB=90°,
∴∠EAD+∠EDA=90°,
∵△ABD为等腰直角三角形,
∴AB=AD,∠BAD=90°,
∴∠CAB+∠DAE=90°,
∴∠BAC=∠ADE,
在△ACB与△DEA中,
,
∴△ACB≌△DEA(AAS)
∴DE=AC=4,AE=BC=2,
∴CE=6,
根据勾股定理得:CD=2
;
如图3,过点D作DE⊥CB,垂足为点E,过点A作AF⊥DE,垂足为点F.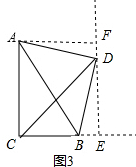
∵∠C=90°,
∴∠CAB+∠CBA=90°,
∵∠DAB+∠DBA=90°,
∴∠EBD+∠DAF=90°,
∵∠EBD+∠BDE=90°,∠DAF+∠ADF=90°,
∴∠DBE=∠ADF,
∵∠BED=∠AFD=90°,DB=AD,
∴△AFD≌△DEB,易求CD=3
.
 解:(1)如图1,△ACB≌△BED;
解:(1)如图1,△ACB≌△BED;∵AC=4,BC=2,AB=2
| 5 |
∴AC2+BC2=AB2,!
∴△ACB为直角三角形,∠ACB=90°,
延长CB,过点D作DE⊥CB于点E,
∵DE⊥CB,
∴∠BED=∠ACB=90°,
∴∠CAB+∠CBA=90°,
∵△ABD为等腰直角三角形,
∴AB=BD,∠ABD=90°,
∴∠CBA+∠DBE=90°,
∴∠CAB=∠EBD,
在△ACB与△BED中,
|
∴△ACB≌△BED(AAS),
∴BE=AC=4,DE=CB=2,
∴CE=6,
根据勾股定理得:CD=2
| 10 |
(2)还有两种,
如图2,过点D作DE⊥CA,垂足为点E.
∵BC⊥CA,

∴∠AED=∠ACB=90°,
∴∠EAD+∠EDA=90°,
∵△ABD为等腰直角三角形,
∴AB=AD,∠BAD=90°,
∴∠CAB+∠DAE=90°,
∴∠BAC=∠ADE,
在△ACB与△DEA中,
|
∴△ACB≌△DEA(AAS)
∴DE=AC=4,AE=BC=2,
∴CE=6,
根据勾股定理得:CD=2
| 13 |
如图3,过点D作DE⊥CB,垂足为点E,过点A作AF⊥DE,垂足为点F.

∵∠C=90°,
∴∠CAB+∠CBA=90°,
∵∠DAB+∠DBA=90°,
∴∠EBD+∠DAF=90°,
∵∠EBD+∠BDE=90°,∠DAF+∠ADF=90°,
∴∠DBE=∠ADF,
∵∠BED=∠AFD=90°,DB=AD,
∴△AFD≌△DEB,易求CD=3
| 2 |
点评:此题考查了全等三角形的判定与性质,熟练掌握全等三角形的判定与性质是解本题的关键.

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案
相关题目

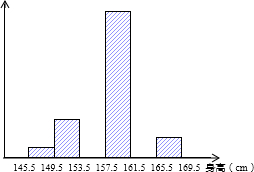 为了解某学校八年级学生的身体发育情况,学校对八年级女生的身高进行了一次测量,所得数据整理后绘制出统计图(如图).
为了解某学校八年级学生的身体发育情况,学校对八年级女生的身高进行了一次测量,所得数据整理后绘制出统计图(如图). 如图,AC与BD相交于点O,且OA=OC,OD=OB,则AD与BC的位置关系是
如图,AC与BD相交于点O,且OA=OC,OD=OB,则AD与BC的位置关系是