题目内容
11.在直角坐标系中,下面各点按顺序依次排列:(0,1),(1,0),(0,-1),(0,2),(2,0),(0,-2),(0,3),(3,0),(0,-3),…
(1)这列点中的第1000个点的坐标是什么?
(2)(0,2012)是这列点中的第几个点?
分析 (1)观察各点规律发现:第1、4、7、10个点在y轴正半轴上,坐标分别(0,1),(0,2),(0,3),(0,4),…,第2、5、8个点在x轴正半轴上,坐标分别(1,0),(2,0),(3,0),…,第3、6、9个点在y轴负半轴上,坐标分别(0,-1),(0,-2),(0,-3),…,依此规律可求出第1000个点的坐标;
(2)根据(1)的规律列出方程即可得解.
解答 解:观察各点规律发现:第1、4、7、10个点在y轴正半轴上,坐标分别(0,1),(0,2),(0,3),(0,4),…,第2、5、8个点在x轴正半轴上,坐标分别(1,0),(2,0),(3,0),…,第3、6、9个点在y轴负半轴上,坐标分别(0,-1),(0,-2),(0,-3),…,
∵1000÷3=333余1,
∴第1000个点在y轴正半轴上,坐标为(0,334).
(2)根据(1)的规律知点(0,2012)在y轴正半轴上,
设它是第n个点,则$\frac{n-1}{3}+1=2012$,解得:n=6034.
所以(0,2012)是这列点中的第6034个点.
点评 此题主要考查了点的变化规律,此题的考点在于对坐平面直角坐标系的熟练运用能力,学生也可从其它方面入手寻找规律.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
19.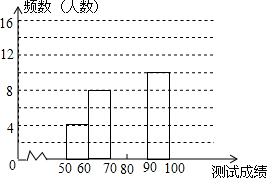 为了提高学生书写汉字的能力,增强保护汉字的意识,我市举办了首届“汉字听写大赛”.现有50名学生参加决赛,他们同时听写50个汉字,每正确听写出一个汉字得2分,根据测试成绩绘制出部分频数分布表和频数分布直方图:
为了提高学生书写汉字的能力,增强保护汉字的意识,我市举办了首届“汉字听写大赛”.现有50名学生参加决赛,他们同时听写50个汉字,每正确听写出一个汉字得2分,根据测试成绩绘制出部分频数分布表和频数分布直方图:
请结合图表完成下列各题:
(1)求表中a的值;
(2)请把频数分布直方图补充完整;
(3)若测试成绩不低于80分为优秀,则本次测试的优秀率是多少?
 为了提高学生书写汉字的能力,增强保护汉字的意识,我市举办了首届“汉字听写大赛”.现有50名学生参加决赛,他们同时听写50个汉字,每正确听写出一个汉字得2分,根据测试成绩绘制出部分频数分布表和频数分布直方图:
为了提高学生书写汉字的能力,增强保护汉字的意识,我市举办了首届“汉字听写大赛”.现有50名学生参加决赛,他们同时听写50个汉字,每正确听写出一个汉字得2分,根据测试成绩绘制出部分频数分布表和频数分布直方图:| 组别 | 成绩x分 | 频数(人数) |
| 第1组 | 50≤x<60 | 4 |
| 第2组 | 60≤x<70 | 8 |
| 第3组 | 70≤x<80 | 16 |
| 第4组 | 80≤x<90 | a |
| 第5组 | 90≤x<100 | 10 |
| 合计 | 50 |
(1)求表中a的值;
(2)请把频数分布直方图补充完整;
(3)若测试成绩不低于80分为优秀,则本次测试的优秀率是多少?
20.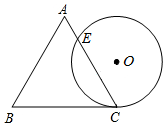 如图,一个边长为4cm的等边三角形ABC的高与⊙O的直径相等.⊙O与BC相切于点C,与AC相交于点E,则CE的长为( )
如图,一个边长为4cm的等边三角形ABC的高与⊙O的直径相等.⊙O与BC相切于点C,与AC相交于点E,则CE的长为( )
 如图,一个边长为4cm的等边三角形ABC的高与⊙O的直径相等.⊙O与BC相切于点C,与AC相交于点E,则CE的长为( )
如图,一个边长为4cm的等边三角形ABC的高与⊙O的直径相等.⊙O与BC相切于点C,与AC相交于点E,则CE的长为( )| A. | 4cm | B. | 3cm | C. | 2cm | D. | 1.5cm |
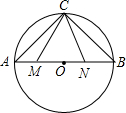 如图,线段AB是半径为6.5的⊙O的直径,点C是弧AB的中点,点M、N在线段AB上,MN=6,若∠MCN=45°,线段AM的长度为$\frac{7+\sqrt{23}}{2}$或$\frac{7-\sqrt{23}}{2}$.
如图,线段AB是半径为6.5的⊙O的直径,点C是弧AB的中点,点M、N在线段AB上,MN=6,若∠MCN=45°,线段AM的长度为$\frac{7+\sqrt{23}}{2}$或$\frac{7-\sqrt{23}}{2}$.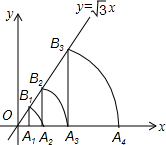 如图,已知直线y=$\sqrt{3}$x,点A1的坐标为(1,0),过点A1作x轴的垂线交直线于点B1,以原点O为圆心,OB1的长为半径画弧交x轴于点A2;再过点A2作x轴的垂线交直线于点B2,以原点O为圆心,OB2的长为半径画弧交x轴于点A3,…,按此做法进行下去,则点B6的坐标为(32,32$\sqrt{3}$).
如图,已知直线y=$\sqrt{3}$x,点A1的坐标为(1,0),过点A1作x轴的垂线交直线于点B1,以原点O为圆心,OB1的长为半径画弧交x轴于点A2;再过点A2作x轴的垂线交直线于点B2,以原点O为圆心,OB2的长为半径画弧交x轴于点A3,…,按此做法进行下去,则点B6的坐标为(32,32$\sqrt{3}$).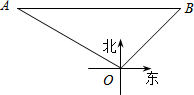 在海上某固定观测点O处的北偏西60°方向,且距离O处40海里的A处,有一艘货轮正沿着正东方向匀速航行,2小时后,此货轮到达O处的北偏东45°方向的B处.在该货轮从A处到B处的航行过程中.
在海上某固定观测点O处的北偏西60°方向,且距离O处40海里的A处,有一艘货轮正沿着正东方向匀速航行,2小时后,此货轮到达O处的北偏东45°方向的B处.在该货轮从A处到B处的航行过程中. 已知,二次函数的解析式为y=-x2+2x+3.
已知,二次函数的解析式为y=-x2+2x+3.