题目内容
6.如图,A,B,C,D为圆O的四等分点,动点P从圆心O出发,沿O-C-D-O-C-D-O路线作匀速运动,设运动时间为x(秒),∠APB的度数为y(度),右图函数图象表示y与x之间函数关系,则点M的横坐标应为( )
| A. | 2 | B. | $\frac{π}{2}$ | C. | $\frac{π}{2}$+1 | D. | $\frac{π}{2}$+3 |
分析 通过函数图象可以得到函数随自变量的变化规律,通过规律结合图象可以求出关键点C、D的坐标值,从而求出M横坐标的值.
解答 解:根据题意,可知点P从圆心O出发,运动到点C时,∠APB的度数由90°减小到45°,
∴在C点时所对的横坐标为1,
∴OC=1,由弧长公式可以求出弧CD的长度为$\frac{1}{2}$π.
∴D点横坐标为:OC+弧CD的长,
∴M的横坐标=OC+弧CD的长+OD+OC=$\frac{1}{2}$π+3.
故选:D.
点评 本题考查了动点问题的函数图象,根据速度、路程、时间的关系求出点P在CD弧上运动的时间是解题的关键,有一定难度.

练习册系列答案
相关题目
5.要清楚地表示出个部分在总体积中所占的百分比,应选择( )
| A. | 条形统计图 | B. | 折线统计图 | C. | 扇形统计图 | D. | 上述3种都可以 |
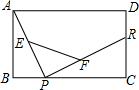 如图,已知矩形ABCD中,R是边CD的中点,P是边BC上一动点,E、F分别是AP、RP的中点,设BP的长为x,EF的长为y,当P在BC上从B向C移动时,y与x的大致图象是( )
如图,已知矩形ABCD中,R是边CD的中点,P是边BC上一动点,E、F分别是AP、RP的中点,设BP的长为x,EF的长为y,当P在BC上从B向C移动时,y与x的大致图象是( )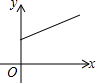
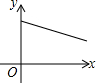
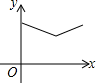
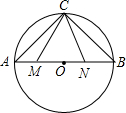 如图,线段AB是半径为6.5的⊙O的直径,点C是弧AB的中点,点M、N在线段AB上,MN=6,若∠MCN=45°,线段AM的长度为$\frac{7+\sqrt{23}}{2}$或$\frac{7-\sqrt{23}}{2}$.
如图,线段AB是半径为6.5的⊙O的直径,点C是弧AB的中点,点M、N在线段AB上,MN=6,若∠MCN=45°,线段AM的长度为$\frac{7+\sqrt{23}}{2}$或$\frac{7-\sqrt{23}}{2}$.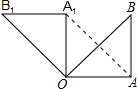 如图所示,在Rt△OAB中,∠OAB=90°,OA=AB=5,将△OAB绕点O沿逆时针方向旋转90°得到△OA1B1.
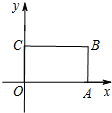
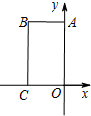
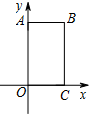
如图所示,在Rt△OAB中,∠OAB=90°,OA=AB=5,将△OAB绕点O沿逆时针方向旋转90°得到△OA1B1.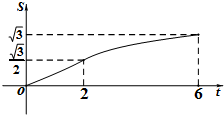 在平面直角坐标系xOy中,四边形OABC是矩形,且A,C在坐标轴上,满足OA=$\sqrt{3}$,OC=1.将矩形OABC绕原点0以每秒15°的速度逆时针旋转.设运动时间为t秒(0≤t≤6),旋转过程中矩形在第二象限内的面积为S,表示S与t的函数关系的图象大致如图所示,则矩形OABC的初始位置是( )
在平面直角坐标系xOy中,四边形OABC是矩形,且A,C在坐标轴上,满足OA=$\sqrt{3}$,OC=1.将矩形OABC绕原点0以每秒15°的速度逆时针旋转.设运动时间为t秒(0≤t≤6),旋转过程中矩形在第二象限内的面积为S,表示S与t的函数关系的图象大致如图所示,则矩形OABC的初始位置是( )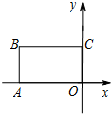
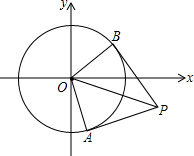 如图,⊙O的半径为1,点P(a,a-4)为⊙O外一点,过点P作⊙O的两条切线,切点分别为点A和点B,则四边形PBOA面积的最小值是$\sqrt{7}$.
如图,⊙O的半径为1,点P(a,a-4)为⊙O外一点,过点P作⊙O的两条切线,切点分别为点A和点B,则四边形PBOA面积的最小值是$\sqrt{7}$. 已知,二次函数的解析式为y=-x2+2x+3.
已知,二次函数的解析式为y=-x2+2x+3.