题目内容
16.在平面直角坐标系中,点($\sqrt{3}$,1)绕原点顺时针旋转60°后得到点( )| A. | ($\sqrt{3}$,-1) | B. | (-1,$\sqrt{3}$) | C. | (-$\sqrt{3}$,1) | D. | (1,-$\sqrt{3}$) |
分析 设A($\sqrt{3}$,1),过A作AB⊥x轴于B,于是得到AB=1,OB=$\sqrt{3}$,根据边角关系得到∠AOB=30°,由于点($\sqrt{3}$,1)绕原点顺时针旋转60°,于是得到∠AOA′=60°,得到∠A′OB=30°,于是结论即可求出.
解答  解:设A($\sqrt{3}$,1),
解:设A($\sqrt{3}$,1),
过A作AB⊥x轴于B,
则AB=1,OB=$\sqrt{3}$,
∴tan∠AOB=$\frac{AB}{OB}=\frac{1}{\sqrt{3}}$=$\frac{\sqrt{3}}{3}$,
∴∠AOB=30°,
∵点($\sqrt{3}$,1)绕原点顺时针旋转60°,
∴∠AOA′=60°,
∴∠A′OB=30°,
∴点($\sqrt{3}$,1)绕原点顺时针旋转60°后得到点是($\sqrt{3}$,-1),
故选A.
点评 本题考查了坐标与图形的变换-旋转,特殊角的三角函数,正确的画出图形是解题的关键.

练习册系列答案
相关题目
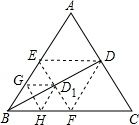 如图,△ABC是边长为1的等边三角形,BD为AC边上的高,将△ABC折叠,使点B与点D重合,折痕EF交BD于点D1,再将△BEF折叠,使点B于点D1重合,折痕GH交BD1于点D2,依次折叠,则BDn=$\frac{\sqrt{3}}{{2}^{n+1}}$.
如图,△ABC是边长为1的等边三角形,BD为AC边上的高,将△ABC折叠,使点B与点D重合,折痕EF交BD于点D1,再将△BEF折叠,使点B于点D1重合,折痕GH交BD1于点D2,依次折叠,则BDn=$\frac{\sqrt{3}}{{2}^{n+1}}$.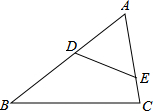 △ABC中,点D,E分别在AB,AC上,∠AED=∠B,如果AE=2,△ADE的面积为4,四边形BCED的面积为5,求边AB的长.
△ABC中,点D,E分别在AB,AC上,∠AED=∠B,如果AE=2,△ADE的面积为4,四边形BCED的面积为5,求边AB的长.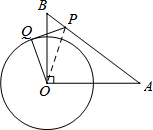 如图,在Rt△OAB中,∠AOB=90°,OA=4,OB=3.⊙O的半径为2,点P是线段AB上的一动点,过点P作⊙O的一条切线PQ,Q为切点.设AP=x,PQ2=y,则y与x的函数图象大致是( )
如图,在Rt△OAB中,∠AOB=90°,OA=4,OB=3.⊙O的半径为2,点P是线段AB上的一动点,过点P作⊙O的一条切线PQ,Q为切点.设AP=x,PQ2=y,则y与x的函数图象大致是( )


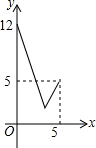
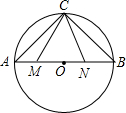 如图,线段AB是半径为6.5的⊙O的直径,点C是弧AB的中点,点M、N在线段AB上,MN=6,若∠MCN=45°,线段AM的长度为$\frac{7+\sqrt{23}}{2}$或$\frac{7-\sqrt{23}}{2}$.
如图,线段AB是半径为6.5的⊙O的直径,点C是弧AB的中点,点M、N在线段AB上,MN=6,若∠MCN=45°,线段AM的长度为$\frac{7+\sqrt{23}}{2}$或$\frac{7-\sqrt{23}}{2}$.
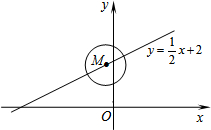 ⊙M的圆心在一次函数y=$\frac{1}{2}$x+2图象上,半径为1.当⊙M与y轴相切时,点M的坐标为(1,$\frac{5}{2}$)或(-1,$\frac{3}{2}$).
⊙M的圆心在一次函数y=$\frac{1}{2}$x+2图象上,半径为1.当⊙M与y轴相切时,点M的坐标为(1,$\frac{5}{2}$)或(-1,$\frac{3}{2}$).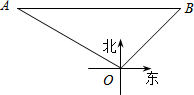 在海上某固定观测点O处的北偏西60°方向,且距离O处40海里的A处,有一艘货轮正沿着正东方向匀速航行,2小时后,此货轮到达O处的北偏东45°方向的B处.在该货轮从A处到B处的航行过程中.
在海上某固定观测点O处的北偏西60°方向,且距离O处40海里的A处,有一艘货轮正沿着正东方向匀速航行,2小时后,此货轮到达O处的北偏东45°方向的B处.在该货轮从A处到B处的航行过程中.