题目内容
10.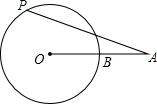 如图,已知线段OA交⊙O于点B,且OB=AB,点P是⊙O上的一个动点,那么∠OAP的最大值是30°.
如图,已知线段OA交⊙O于点B,且OB=AB,点P是⊙O上的一个动点,那么∠OAP的最大值是30°.
分析 当AP与⊙O相切时,∠OAP有最大值,连结OP,根据切线的性质得OP⊥AP,由OB=AB得OA=2OP,然后根据含30度的直角三角形三边的关系即可得到此时∠OAP的度数.
解答  解:当AP与⊙O相切时,∠OAP有最大值,连结OP,如图,
解:当AP与⊙O相切时,∠OAP有最大值,连结OP,如图,
则OP⊥AP,
∵OB=AB,
∴OA=2OP,
∴sin∠PAO=$\frac{OP}{OA}$=$\frac{1}{2}$,
∴∠PAO=30°,
故答案为:30°.
点评 本题考查了切线的性质:圆的切线垂直于过切点的半径.也考查了含30度的直角三角形三边的关系,知道当AP与⊙O相切时,∠OAP有最大值是解题的关键.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
9.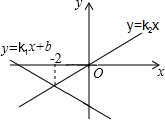 同一直角坐标系中,一次函数y1=k1x+b与正比例函数y2=k2x的图象如图所示,则满足y1≥y2的x取值范围是( )
同一直角坐标系中,一次函数y1=k1x+b与正比例函数y2=k2x的图象如图所示,则满足y1≥y2的x取值范围是( )
 同一直角坐标系中,一次函数y1=k1x+b与正比例函数y2=k2x的图象如图所示,则满足y1≥y2的x取值范围是( )
同一直角坐标系中,一次函数y1=k1x+b与正比例函数y2=k2x的图象如图所示,则满足y1≥y2的x取值范围是( )| A. | x≤-2 | B. | x≥-2 | C. | x<-2 | D. | x>-2 |
19.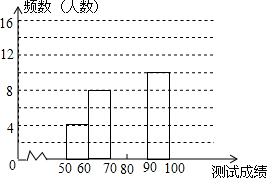 为了提高学生书写汉字的能力,增强保护汉字的意识,我市举办了首届“汉字听写大赛”.现有50名学生参加决赛,他们同时听写50个汉字,每正确听写出一个汉字得2分,根据测试成绩绘制出部分频数分布表和频数分布直方图:
为了提高学生书写汉字的能力,增强保护汉字的意识,我市举办了首届“汉字听写大赛”.现有50名学生参加决赛,他们同时听写50个汉字,每正确听写出一个汉字得2分,根据测试成绩绘制出部分频数分布表和频数分布直方图:
请结合图表完成下列各题:
(1)求表中a的值;
(2)请把频数分布直方图补充完整;
(3)若测试成绩不低于80分为优秀,则本次测试的优秀率是多少?
 为了提高学生书写汉字的能力,增强保护汉字的意识,我市举办了首届“汉字听写大赛”.现有50名学生参加决赛,他们同时听写50个汉字,每正确听写出一个汉字得2分,根据测试成绩绘制出部分频数分布表和频数分布直方图:
为了提高学生书写汉字的能力,增强保护汉字的意识,我市举办了首届“汉字听写大赛”.现有50名学生参加决赛,他们同时听写50个汉字,每正确听写出一个汉字得2分,根据测试成绩绘制出部分频数分布表和频数分布直方图:| 组别 | 成绩x分 | 频数(人数) |
| 第1组 | 50≤x<60 | 4 |
| 第2组 | 60≤x<70 | 8 |
| 第3组 | 70≤x<80 | 16 |
| 第4组 | 80≤x<90 | a |
| 第5组 | 90≤x<100 | 10 |
| 合计 | 50 |
(1)求表中a的值;
(2)请把频数分布直方图补充完整;
(3)若测试成绩不低于80分为优秀,则本次测试的优秀率是多少?
20.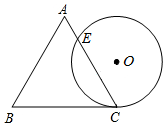 如图,一个边长为4cm的等边三角形ABC的高与⊙O的直径相等.⊙O与BC相切于点C,与AC相交于点E,则CE的长为( )
如图,一个边长为4cm的等边三角形ABC的高与⊙O的直径相等.⊙O与BC相切于点C,与AC相交于点E,则CE的长为( )
 如图,一个边长为4cm的等边三角形ABC的高与⊙O的直径相等.⊙O与BC相切于点C,与AC相交于点E,则CE的长为( )
如图,一个边长为4cm的等边三角形ABC的高与⊙O的直径相等.⊙O与BC相切于点C,与AC相交于点E,则CE的长为( )| A. | 4cm | B. | 3cm | C. | 2cm | D. | 1.5cm |
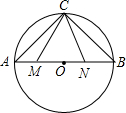 如图,线段AB是半径为6.5的⊙O的直径,点C是弧AB的中点,点M、N在线段AB上,MN=6,若∠MCN=45°,线段AM的长度为$\frac{7+\sqrt{23}}{2}$或$\frac{7-\sqrt{23}}{2}$.
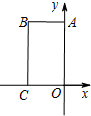
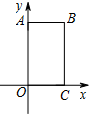
如图,线段AB是半径为6.5的⊙O的直径,点C是弧AB的中点,点M、N在线段AB上,MN=6,若∠MCN=45°,线段AM的长度为$\frac{7+\sqrt{23}}{2}$或$\frac{7-\sqrt{23}}{2}$.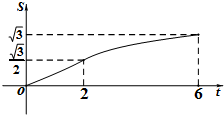 在平面直角坐标系xOy中,四边形OABC是矩形,且A,C在坐标轴上,满足OA=$\sqrt{3}$,OC=1.将矩形OABC绕原点0以每秒15°的速度逆时针旋转.设运动时间为t秒(0≤t≤6),旋转过程中矩形在第二象限内的面积为S,表示S与t的函数关系的图象大致如图所示,则矩形OABC的初始位置是( )
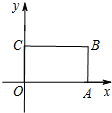
在平面直角坐标系xOy中,四边形OABC是矩形,且A,C在坐标轴上,满足OA=$\sqrt{3}$,OC=1.将矩形OABC绕原点0以每秒15°的速度逆时针旋转.设运动时间为t秒(0≤t≤6),旋转过程中矩形在第二象限内的面积为S,表示S与t的函数关系的图象大致如图所示,则矩形OABC的初始位置是( )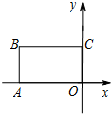
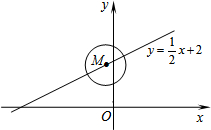 ⊙M的圆心在一次函数y=$\frac{1}{2}$x+2图象上,半径为1.当⊙M与y轴相切时,点M的坐标为(1,$\frac{5}{2}$)或(-1,$\frac{3}{2}$).
⊙M的圆心在一次函数y=$\frac{1}{2}$x+2图象上,半径为1.当⊙M与y轴相切时,点M的坐标为(1,$\frac{5}{2}$)或(-1,$\frac{3}{2}$).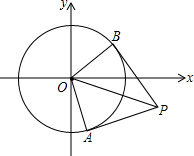 如图,⊙O的半径为1,点P(a,a-4)为⊙O外一点,过点P作⊙O的两条切线,切点分别为点A和点B,则四边形PBOA面积的最小值是$\sqrt{7}$.
如图,⊙O的半径为1,点P(a,a-4)为⊙O外一点,过点P作⊙O的两条切线,切点分别为点A和点B,则四边形PBOA面积的最小值是$\sqrt{7}$.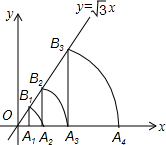 如图,已知直线y=$\sqrt{3}$x,点A1的坐标为(1,0),过点A1作x轴的垂线交直线于点B1,以原点O为圆心,OB1的长为半径画弧交x轴于点A2;再过点A2作x轴的垂线交直线于点B2,以原点O为圆心,OB2的长为半径画弧交x轴于点A3,…,按此做法进行下去,则点B6的坐标为(32,32$\sqrt{3}$).
如图,已知直线y=$\sqrt{3}$x,点A1的坐标为(1,0),过点A1作x轴的垂线交直线于点B1,以原点O为圆心,OB1的长为半径画弧交x轴于点A2;再过点A2作x轴的垂线交直线于点B2,以原点O为圆心,OB2的长为半径画弧交x轴于点A3,…,按此做法进行下去,则点B6的坐标为(32,32$\sqrt{3}$).