题目内容
1.如图是由一些大小相同的小正方体组成的简单几何体的主视图和俯视图.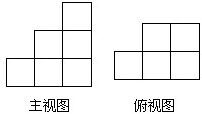
(1)请画出这个几何体的左视图(有多种);
(2)若组成这个几何体的小正方体的块数为n,请写出n所有可能的值(不必说理由);最多共有多少种不同的组合方法?
分析 (1)根据主视图可知可能有三列,由俯视图可知应有5列,即可得出所有的组成图形,即可得出左视图;
(2)从俯视图中可以看出最底层小正方体的个数及形状,从主视图可以看出每一层小正方体的层数和个数;根据主视图、左视图、俯视图是分别从物体正面、左面和上面看,所得到的图形,再根据主视图与俯视图得出答案.
解答 解:(1)如图所示: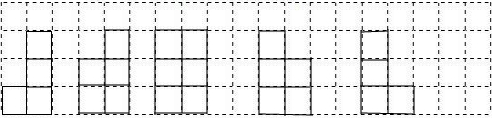
(2)主视图最右边可能有4或5或6个小正方体;
由主视图最左边看到只有一列,俯视图也只有一列,则左边有一个小正方体;
主视图中间有两列,俯视图亦有两列,则中间可以有3或4个小正方形.
则n的值可能为:1+4+3=8,1+5+3=9,1+6+3=10,1+4+4=9,1+5+4=10,1+6+4=11,
根据几何体的主视图和俯视图,可以得出从主视图看最少有6个,从俯视图看,最左边正方形前后可以有三列,分别有三个,
则最多有3×3+3=12种不同的组合方法.
点评 此题主要考查了左视图以及由三视图判断几何体的形状,主要培养同学们的空间想象能力,想象不出来可以亲手实验.

练习册系列答案
相关题目
3.石家庄地铁工程于2012年9月28如正式开工建设,到2020年将建成轨道交通1、2、3号线一期工程,其中1号线一期工程轨道全长约23900m,用科学记数法表示1号线一期工程的轨道全长是( )
| A. | 0.239×105m | B. | 2.39×105m | C. | 2.39×104m | D. | 23.9×103m |
11.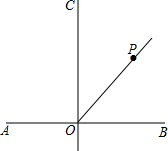 如图,直线AB⊥CD,垂足为O,点P在∠BOC的平分线上,点E在直线AB上,且△EOP是等腰三角形,则这样的点P有( )
如图,直线AB⊥CD,垂足为O,点P在∠BOC的平分线上,点E在直线AB上,且△EOP是等腰三角形,则这样的点P有( )
 如图,直线AB⊥CD,垂足为O,点P在∠BOC的平分线上,点E在直线AB上,且△EOP是等腰三角形,则这样的点P有( )
如图,直线AB⊥CD,垂足为O,点P在∠BOC的平分线上,点E在直线AB上,且△EOP是等腰三角形,则这样的点P有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
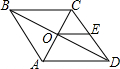 如图,已知菱形ABCD的对角线AC、BD相交于点O,AB=6cm,E是CD的中点,则OE的长为3cm.
如图,已知菱形ABCD的对角线AC、BD相交于点O,AB=6cm,E是CD的中点,则OE的长为3cm.
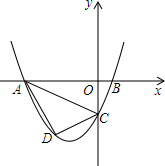 已知,如图抛物线y=ax2+3ax+c(a>0)与y轴交于点C,与x轴交于A,B两点,点A在点B左侧.点B的坐标为(1,0),OC=3OB.
已知,如图抛物线y=ax2+3ax+c(a>0)与y轴交于点C,与x轴交于A,B两点,点A在点B左侧.点B的坐标为(1,0),OC=3OB.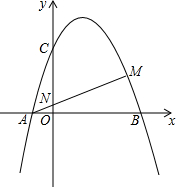 如图,抛物线y=-x2+2x+3与x轴交于A、B两点,M为第一象限的抛物线上一点,AM交y轴于N,且AM•AN=4.
如图,抛物线y=-x2+2x+3与x轴交于A、B两点,M为第一象限的抛物线上一点,AM交y轴于N,且AM•AN=4.