题目内容
13. 如图,△ABC中,O为外心,三条高AD、BE、CF交于点H,直线ED和AB交于点M,FD和AC交于点N.求证:OH⊥MN.
如图,△ABC中,O为外心,三条高AD、BE、CF交于点H,直线ED和AB交于点M,FD和AC交于点N.求证:OH⊥MN.
分析 由AD、BE、CF分别是△ABC的高,可得A、C、D、F四点共圆,AC为直径,进而由圆内接四边形性质得到∠BDF=∠BAC,由O为△ABC外心,可得∠OBC=$\frac{1}{2}$(180°-∠BOC)=90°-∠BAC=90°-∠FDB,进而得到结论.
解答 证明:∵A、C、D、F四点共圆,
∴∠BDF=∠BAC
又∵∠OBC=$\frac{1}{2}$(180°-∠BOC)=90°-∠BAC,
∴OB⊥DF.
∵CF⊥MA,
∴MC2-MH2=AC2-AH2(①)
∵BE⊥NA,
∴NB2-NH2=AB2-AH2 (②)
∵DA⊥BC,
∴BD2-CD2=BA2-AC2 (③)
∵OB⊥DF,
∴BN2-BD2=ON2-OD2 (④)
∵OC⊥DE,
∴CM2-CD2=OM2-OD2,
①-②+③+④-⑤,得NH2-MH2=ON2-OM2 MO2-MH2=NO2-NH2
∴OH⊥MN.
点评 主要考查了圆周角定理和三角形的外角和内角关系,其中分析出A、C、D、F四点共圆,是解答的关键.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
5.若不等式组$\left\{\begin{array}{l}{x-b≤0}\\{x+a>0}\end{array}\right.$的解集为2<x≤3,则a,b的值分别为( )
| A. | -2,3 | B. | 2,-3 | C. | 3,-2 | D. | -3,2 |
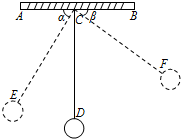 如图,物理实验室有一单摆在左右摆动,摆动过程中选取了两个瞬时状态,从C处测得E、F两点的俯角分别为∠ACE=α,∠BCF=β,这时点F相对于点E升高了acm.求该摆绳CD的长度.(用含a、α、β的式子表示)
如图,物理实验室有一单摆在左右摆动,摆动过程中选取了两个瞬时状态,从C处测得E、F两点的俯角分别为∠ACE=α,∠BCF=β,这时点F相对于点E升高了acm.求该摆绳CD的长度.(用含a、α、β的式子表示)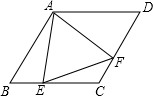 如图,在菱形ABCD中,∠B=60°,若AB=2,点E是BC边上一动点,∠EAF=60°,AF交CD于点F
如图,在菱形ABCD中,∠B=60°,若AB=2,点E是BC边上一动点,∠EAF=60°,AF交CD于点F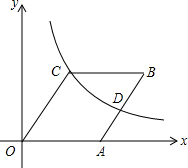 如图,在菱形OABC中点A在x轴的正半轴上,点B坐标为(8,4)双曲线y=$\frac{k}{x}$(k>0)经过点C,交AB于点D.
如图,在菱形OABC中点A在x轴的正半轴上,点B坐标为(8,4)双曲线y=$\frac{k}{x}$(k>0)经过点C,交AB于点D.