题目内容
12．
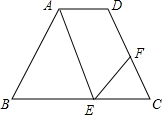如图，AD∥BC，∠EAD=∠C，∠FEC=∠BAE，∠EFC=50°（1）求证：AE∥CD；
（2）求∠B的度数．
分析 （1）根据平行线的性质和等量关系可得∠EAD+∠D=180°，根据同旁内角互补，两直线平行即可证明；
（2）根据平行线的性质可得∠AEB=∠C，根据三角形内角和定理和等量关系即可得到∠B的度数．
解答 （1）证明：∵AD∥BC，
∴∠D+∠C=180°，
∵∠EAD=∠C，
∴∠EAD+∠D=180°，
∴AE∥CD；
（2）∵AE∥CD，
∴∠AEB=∠C，
∵∠FEC=∠BAE，
∴∠B=∠EFC=50°．
点评 考查了平行线的判定和性质，三角形内角和定理，解题的关键是证明AE∥CD．
练习册系列答案
学业测评一课一测系列答案
相关题目
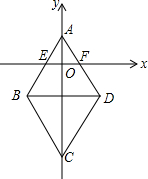已知：如图，菱形ABCD中，已知点A（0，4）和C（0，-12），边AD交x轴于点F（3，0），求点B、D的坐标．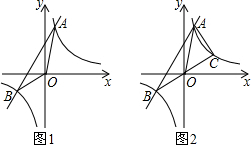
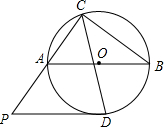如图，△ABC内接于⊙O，且AB为⊙O的直径，过CA延长线上点P作⊙O的切线PD．切点为D，且PD∥AB．
7．已知函数y=$\sqrt{x+1}$，则自变量x的取值范围是（ ）
| A． | x＜-1 | B． | x＞-1 | C． | x≤-1 | D． | x≥-1 |
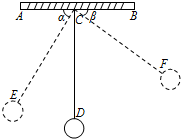如图，物理实验室有一单摆在左右摆动，摆动过程中选取了两个瞬时状态，从C处测得E、F两点的俯角分别为∠ACE=α，∠BCF=β，这时点F相对于点E升高了acm．求该摆绳CD的长度．（用含a、α、β的式子表示）
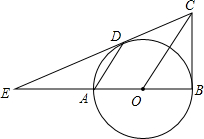如图，已知AB是⊙O的直径，BC⊥AB，连接OC，弦AD∥OC，直线CD交BA的延长线于点E．
7．已知圆上均匀分布着2000个点，从中均等地选出A、B、C、D四个不同的点，则弦AB与CD相交的概率是（ ）
| A． | $\frac{2}{3}$ | B． | $\frac{1}{4}$ | C． | $\frac{1}{2}$ | D． | $\frac{1}{3}$ |
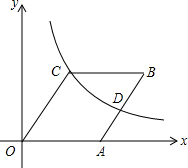如图，在菱形OABC中点A在x轴的正半轴上，点B坐标为（8，4）双曲线y=$\frac{k}{x}$（k＞0）经过点C，交AB于点D．