题目内容
8.有十张正面分别标有数字-10、-9、-8、-7、-6、-5、-4、-3、-2、-1的不透明卡片,它们除数字不同外其余全部相同,将它们背面朝上,洗匀后从中任取一张,以卡片上的数字作为关于x的不等式ax+b>0中的系数a,如果该不等式有正整数解的概率为$\frac{1}{2}$,则b的取值范围是5<b≤6.分析 根据a的正负性解不等式,结合其有正整数解的概率可得a的值,进而可得关于b的不等式,求解可得.
解答 解:∵a<0,
∴不等式ax+b>0的解集为x<-$\frac{b}{a}$,
∵该不等式有正整数解的概率为$\frac{1}{2}$,
∴当a=-1、-2、-3、-4、-5时,该不等式有正整数解,当a=-6时,不等式没有正整数解,
∴$\frac{b}{5}>1$,且$\frac{b}{6}$≤1,
∴5<b≤6,
故答案为:5<b≤6.
点评 此题考查了概率公式的应用以及不等式的解的情况.用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
相关题目
18.关于x的一元二次方程x2-2x+1=0的根的情况是( )
| A. | 有两个不相等的实数根 | B. | 有两个相等的实根 | ||
| C. | 没有实数根 | D. | 不能确定 |
19.我国雾霾天气多发,PM2.5颗粒被称为大气污染的元凶,PM2.5是指直径小于或等于2.5微米的颗粒物,即0.0000025米的颗粒物,将0.0000025用科学记数法表示为( )
| A. | 2.5×10-7 | B. | 25×10-7 | C. | 2.5×10-6 | D. | 0.25×10-5 |
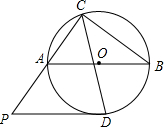 如图,△ABC内接于⊙O,且AB为⊙O的直径,过CA延长线上点P作⊙O的切线PD.切点为D,且PD∥AB.
如图,△ABC内接于⊙O,且AB为⊙O的直径,过CA延长线上点P作⊙O的切线PD.切点为D,且PD∥AB.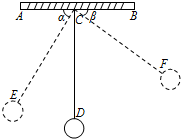 如图,物理实验室有一单摆在左右摆动,摆动过程中选取了两个瞬时状态,从C处测得E、F两点的俯角分别为∠ACE=α,∠BCF=β,这时点F相对于点E升高了acm.求该摆绳CD的长度.(用含a、α、β的式子表示)
如图,物理实验室有一单摆在左右摆动,摆动过程中选取了两个瞬时状态,从C处测得E、F两点的俯角分别为∠ACE=α,∠BCF=β,这时点F相对于点E升高了acm.求该摆绳CD的长度.(用含a、α、β的式子表示)