题目内容
9.若多项式mx4+x3+nx-3含有因式(x+1)和(x-1),则mn的值为-3.分析 根据多项式的因式结合多项式的系数可判断另外的因式,根据整式乘法可得对应系数相等,从而得m、n的值.
解答 解:(x+1)(x-1)=x2-1,
∵由多项式mx4+x3+nx-3含有因式x-1与x+1,且4次项系数为m,3次项系数为1,常数项是-3,
∴mx4+x3+nx-3=(x2-1)(mx2+x+3),
即mx4+x3+nx-3=mx4+x3+(3-m)x2-x-3,
∴3-m=0,n=-1,
解得:m=3,n=-1,
则mn=-3,
故答案为:-3.
点评 本题主要考查因式分解的意义,根据系数准确判断另一个因式是解题的关键.

练习册系列答案
相关题目
19.我国雾霾天气多发,PM2.5颗粒被称为大气污染的元凶,PM2.5是指直径小于或等于2.5微米的颗粒物,即0.0000025米的颗粒物,将0.0000025用科学记数法表示为( )
| A. | 2.5×10-7 | B. | 25×10-7 | C. | 2.5×10-6 | D. | 0.25×10-5 |
7.已知圆上均匀分布着2000个点,从中均等地选出A、B、C、D四个不同的点,则弦AB与CD相交的概率是( )
| A. | $\frac{2}{3}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{2}$ | D. | $\frac{1}{3}$ |
5.若不等式组$\left\{\begin{array}{l}{x-b≤0}\\{x+a>0}\end{array}\right.$的解集为2<x≤3,则a,b的值分别为( )
| A. | -2,3 | B. | 2,-3 | C. | 3,-2 | D. | -3,2 |
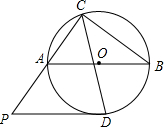 如图,△ABC内接于⊙O,且AB为⊙O的直径,过CA延长线上点P作⊙O的切线PD.切点为D,且PD∥AB.
如图,△ABC内接于⊙O,且AB为⊙O的直径,过CA延长线上点P作⊙O的切线PD.切点为D,且PD∥AB.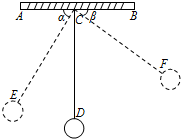 如图,物理实验室有一单摆在左右摆动,摆动过程中选取了两个瞬时状态,从C处测得E、F两点的俯角分别为∠ACE=α,∠BCF=β,这时点F相对于点E升高了acm.求该摆绳CD的长度.(用含a、α、β的式子表示)
如图,物理实验室有一单摆在左右摆动,摆动过程中选取了两个瞬时状态,从C处测得E、F两点的俯角分别为∠ACE=α,∠BCF=β,这时点F相对于点E升高了acm.求该摆绳CD的长度.(用含a、α、β的式子表示)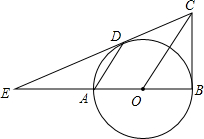 如图,已知AB是⊙O的直径,BC⊥AB,连接OC,弦AD∥OC,直线CD交BA的延长线于点E.
如图,已知AB是⊙O的直径,BC⊥AB,连接OC,弦AD∥OC,直线CD交BA的延长线于点E.