题目内容
7.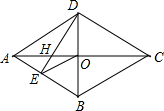 如图,四边形ABCD是菱形,对角线AC与BD相交于点O.DE⊥AB于点E.连接OE.
如图,四边形ABCD是菱形,对角线AC与BD相交于点O.DE⊥AB于点E.连接OE.(1)求证:∠OED=∠ACD;
(2)若AC=8,DB=6,求DH的长.
分析 (1)由四边形ABCD是菱形,DE⊥AB,易得点A,E,O,D共圆,然后由圆周角定理,证得∠OED=∠CAD,继而证得∠OED=∠ACD;
(2)由AC=8,DB=6,利用菱形的面积,可求得DE的长,然后由△AEH∽△AOB,求得EH的长,继而求得答案.
解答 (1)证明:∵四边形ABCD是菱形,
∴AC⊥BD,AD=CD,
∴∠DAC=∠ACD,
∵DE⊥AB,
∴∠AOD=∠AED=90°,
∴点A,E,O,D共圆,
∵∠OED=∠CAD,
∴∠OED=∠ACD;
(2)∵四边形ABCD是菱形,AC=8,DB=6,
∴OA=$\frac{1}{2}$AC=4,OB=$\frac{1}{2}$DB=3,
∴AB=$\sqrt{O{A}^{2}+O{B}^{2}}$=5,
∵S菱形ABCD=$\frac{1}{2}$AC•BD=AB•DE,
∴DE=$\frac{\frac{1}{2}AC•BD}{AB}$=$\frac{24}{5}$;
∴AE=$\sqrt{A{D}^{2}-D{E}^{2}}$=$\frac{7}{5}$,
∵∠AEH=∠AOB=90°,∠EAH=∠OAB,
∴△AEH∽△AOB,
∴AE:AO=EH:OB,
∴$\frac{7}{5}$:4=EH:3,
解得:EH=$\frac{21}{20}$,
∴DH=DE-EH=$\frac{15}{4}$.
点评 此题考查了菱形的性质、相似三角形的判定与性质以及勾股定理.注意证得点A,E,O,D共圆与△AEH∽△AOB是解此题的关键.

练习册系列答案
相关题目
18.关于x的一元二次方程x2-2x+1=0的根的情况是( )
| A. | 有两个不相等的实数根 | B. | 有两个相等的实根 | ||
| C. | 没有实数根 | D. | 不能确定 |
15. 如图,?ABCD的周长为10cm,AE平分∠BAD,若CE=1cm,则AB的长度是( )
如图,?ABCD的周长为10cm,AE平分∠BAD,若CE=1cm,则AB的长度是( )
 如图,?ABCD的周长为10cm,AE平分∠BAD,若CE=1cm,则AB的长度是( )
如图,?ABCD的周长为10cm,AE平分∠BAD,若CE=1cm,则AB的长度是( )| A. | 5cm | B. | 4cm | C. | 3cm | D. | 2cm |
19.我国雾霾天气多发,PM2.5颗粒被称为大气污染的元凶,PM2.5是指直径小于或等于2.5微米的颗粒物,即0.0000025米的颗粒物,将0.0000025用科学记数法表示为( )
| A. | 2.5×10-7 | B. | 25×10-7 | C. | 2.5×10-6 | D. | 0.25×10-5 |
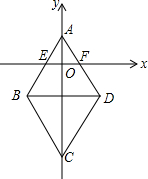 已知:如图,菱形ABCD中,已知点A(0,4)和C(0,-12),边AD交x轴于点F(3,0),求点B、D的坐标.
已知:如图,菱形ABCD中,已知点A(0,4)和C(0,-12),边AD交x轴于点F(3,0),求点B、D的坐标.
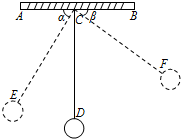 如图,物理实验室有一单摆在左右摆动,摆动过程中选取了两个瞬时状态,从C处测得E、F两点的俯角分别为∠ACE=α,∠BCF=β,这时点F相对于点E升高了acm.求该摆绳CD的长度.(用含a、α、β的式子表示)
如图,物理实验室有一单摆在左右摆动,摆动过程中选取了两个瞬时状态,从C处测得E、F两点的俯角分别为∠ACE=α,∠BCF=β,这时点F相对于点E升高了acm.求该摆绳CD的长度.(用含a、α、β的式子表示)