题目内容
2．
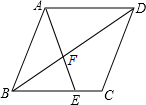如图所示，在菱形ABCD中，E是BC上一点，且AE=AB，∠EAD=2∠BAE．求证：BE=AF．
分析 根据菱形的性质得出AB=AD，AD∥BC，得出∠EAD=∠AEB=∠ABE，设∠BAE=x，根据等腰三角形两底角相等表示出∠ABE，再根据菱形的邻角互补列出方程求解得出∠BAE=36°，∠AEB=∠ABE=∠EAD=72°，求出∠BFE=∠AEB，即可得出结论．
解答 证明：∵在菱形ABCD中，AB=AD，AD∥BC，
∴∠ABD=∠ADB，∠EAD=∠AEB，
∵AB=AE，
∴∠ABE=∠AEB，
∵∠EAD=2∠BAE．
∴∠EAD=∠AEB=∠ABE，
设∠BAE=x，则∠EAD=∠AEB=∠ABE=2x，
∵AD∥BC，
∴∠BAD+∠ABE=180°，
∴x+2x+2x=180°，
解得：x=36°，
∴∠BAE=36°，∠AEB=∠ABE=∠EAD=72°，
∴∠BAD=108°，
∴∠ABD=$\frac{1}{2}$（180°-108°）=36°，
∴∠BFE=36°+36°=72°=∠AEB，
∴BE=AF．
点评 本题考查了菱形的性质，等腰三角形的性质，熟记各性质并列出关于∠BAE的方程是解题的关键．
练习册系列答案
教学练新同步练习系列答案
课前课后同步练习系列答案
课堂小作业系列答案
相关题目
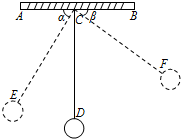如图，物理实验室有一单摆在左右摆动，摆动过程中选取了两个瞬时状态，从C处测得E、F两点的俯角分别为∠ACE=α，∠BCF=β，这时点F相对于点E升高了acm．求该摆绳CD的长度．（用含a、α、β的式子表示）
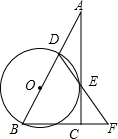如图，在Rt△ABC中，△ACB=90°，D是AB边上的一点，以BD为直径的⊙O与AC相切于点E，连接DE并延长，与BC的延长线交于点F．