题目内容
15.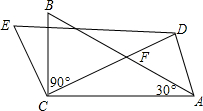 如图所示,在△ABC中,∠ACB=90°,∠A=30°,将△ABC绕点C按逆时针旋转α(0°<α<90°)得△DEC.设CD交AB于点F,当∠ACD=40°或20°时,△ADF为等腰三角形.
如图所示,在△ABC中,∠ACB=90°,∠A=30°,将△ABC绕点C按逆时针旋转α(0°<α<90°)得△DEC.设CD交AB于点F,当∠ACD=40°或20°时,△ADF为等腰三角形.
分析 根据旋转的性质得∠DCA=α,CD=CA,则利用等腰三角形的性质和三角形内角和定理可计算出∠CDA=∠CAD=90°-$\frac{1}{2}$α,根据三角形外角性质得∠DFA=∠FCA+∠FAC=α+30°,当FD=FA,则∠FDA=∠FAD,这不合题意舍去;当AF=AD,则∠ADF=∠AFD,即90°-$\frac{1}{2}$α=30°+α;当DF=DA,则∠DFA=∠DAF,即30°+α=90°-$\frac{1}{2}$α-30°,然后分别解方程即可得到α的值即可.
解答 解:∵△ABC绕C点按逆时针方向旋转α角(0°<α<90°)得到△DEC,
∴∠DCA=α,CD=CA,
∴∠CDA=∠CAD=$\frac{1}{2}$(180°-α)=90°-$\frac{1}{2}$α,
∠DFA=∠FCA+∠FAC=α+30°,
当FD=FA,则∠FDA=∠FAD,这不合题意舍去;
当AF=AD,则∠ADF=∠AFD,即90°-$\frac{1}{2}$α=30°+α,解得α=40°;
当DF=DA,则∠DFA=∠DAF,即30°+α=90°-$\frac{1}{2}$α-30°,解得α=20°.
故答案为40°或20°.
点评 本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.也考查了等腰三角形的判定.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
10.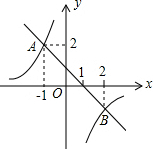 如图,直线y=-x+b与双曲线y=$\frac{k}{x}$交于点A,B,则不等式组$\frac{k}{x}$<-x+b<0的解集为( )
如图,直线y=-x+b与双曲线y=$\frac{k}{x}$交于点A,B,则不等式组$\frac{k}{x}$<-x+b<0的解集为( )
 如图,直线y=-x+b与双曲线y=$\frac{k}{x}$交于点A,B,则不等式组$\frac{k}{x}$<-x+b<0的解集为( )
如图,直线y=-x+b与双曲线y=$\frac{k}{x}$交于点A,B,则不等式组$\frac{k}{x}$<-x+b<0的解集为( )| A. | 0<x<2 | B. | x<-1或0<x<2 | C. | -1<x<2 | D. | 1<x<2 |
20. 如图,把△ABC绕点C逆时针旋转90°得到△DCE,若∠A=35°,则∠ADE为( )
如图,把△ABC绕点C逆时针旋转90°得到△DCE,若∠A=35°,则∠ADE为( )
 如图,把△ABC绕点C逆时针旋转90°得到△DCE,若∠A=35°,则∠ADE为( )
如图,把△ABC绕点C逆时针旋转90°得到△DCE,若∠A=35°,则∠ADE为( )| A. | 35° | B. | 55° | C. | 135° | D. | 125° |
7.下列计算正确的是( )
| A. | (a2)3=a5 | B. | a6÷a6=0 | C. | (-2a)2=-4a2 | D. | a•a5=a6 |
4. 如图,一只青蛙在圆周上标有数字的五个点上跳,若它停在奇数点上,则下一次沿顺时针方向跳两个点;若停在偶数点上,则下一次沿逆时针方向跳一个点.若青蛙从5这点开始跳,则经2013次跳后它停在的点所对应的数为( )
如图,一只青蛙在圆周上标有数字的五个点上跳,若它停在奇数点上,则下一次沿顺时针方向跳两个点;若停在偶数点上,则下一次沿逆时针方向跳一个点.若青蛙从5这点开始跳,则经2013次跳后它停在的点所对应的数为( )
 如图,一只青蛙在圆周上标有数字的五个点上跳,若它停在奇数点上,则下一次沿顺时针方向跳两个点;若停在偶数点上,则下一次沿逆时针方向跳一个点.若青蛙从5这点开始跳,则经2013次跳后它停在的点所对应的数为( )
如图,一只青蛙在圆周上标有数字的五个点上跳,若它停在奇数点上,则下一次沿顺时针方向跳两个点;若停在偶数点上,则下一次沿逆时针方向跳一个点.若青蛙从5这点开始跳,则经2013次跳后它停在的点所对应的数为( )| A. | 1 | B. | 2 | C. | 3 | D. | 5 |
5.不等式组$\left\{\begin{array}{l}3x+6≤0\\ 4-2x≥0\end{array}\right.$的解集是( )
| A. | -4≤x≤2 | B. | x≤-2 | C. | x≥2 | D. | x≤-4 |
 如图,已知菱形ABCD的边长为$\sqrt{6}$,∠ABC=45°,求菱形ABCD的面积.
如图,已知菱形ABCD的边长为$\sqrt{6}$,∠ABC=45°,求菱形ABCD的面积.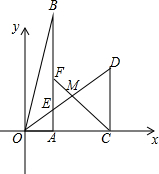 如图,在直角坐标系xOy中,Rt△OAB和Rt△OCD的直角顶点A,C始终在x轴的正半轴上,B,D在第一象限内,点B在直线OD上方,OC=CD,OD=2,M为OD的中点,AB与OD相交于E,当点B位置变化时,Rt△OAB的面积恒为$\frac{1}{2}$.
如图,在直角坐标系xOy中,Rt△OAB和Rt△OCD的直角顶点A,C始终在x轴的正半轴上,B,D在第一象限内,点B在直线OD上方,OC=CD,OD=2,M为OD的中点,AB与OD相交于E,当点B位置变化时,Rt△OAB的面积恒为$\frac{1}{2}$.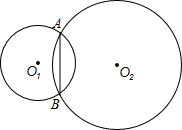 如图,两相交圆的公共弦AB,在⊙O1中为内接正三角形的一边,在⊙O2中为内接正六边形的一边,求这两圆的面积之比.
如图,两相交圆的公共弦AB,在⊙O1中为内接正三角形的一边,在⊙O2中为内接正六边形的一边,求这两圆的面积之比.