题目内容
3.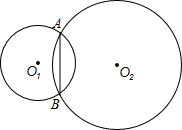 如图,两相交圆的公共弦AB,在⊙O1中为内接正三角形的一边,在⊙O2中为内接正六边形的一边,求这两圆的面积之比.
如图,两相交圆的公共弦AB,在⊙O1中为内接正三角形的一边,在⊙O2中为内接正六边形的一边,求这两圆的面积之比.
分析 根据内接多边形的性质分别求得两圆的半径,然后根据圆的面积公式求这两圆的面积之比.
解答  解:如图,连O1O2交AB于D,交⊙O于C,则O1O2垂直平分AB.
解:如图,连O1O2交AB于D,交⊙O于C,则O1O2垂直平分AB.
∵AB为⊙O2内接正六边形的一边,
∴△O2AB为等边三角形,
设O2A=AB=k.
又∵AB分别为⊙O的内接正三角形,
∴AD=$\frac{1}{2}$k,∠AO1B=2∠ACB=120°,
∴∠AO1D=60°,
∴O1A=$\frac{AD}{sin60°}$=$\frac{\frac{1}{2}k}{\frac{\sqrt{3}}{2}}$=$\frac{\sqrt{3}k}{3}$,
∴这两圆的面积之比为:πO1A2:πO2A2=O1A2:O2A2=$\frac{\sqrt{3}k}{3}$:$\frac{1}{2}$k=2$\sqrt{3}$:3.
点评 本题考查了相交两圆的性质、等边三角形的性质以及解直角三角形.此题实际上求两圆的半径之比.

练习册系列答案
相关题目
18.学校为了了解学生的身高情况,随机抽查了50名学生调查他们的身高,数据经整理制成不完整身高频数分布表:
根据以上信息,回答下列问题:
(1)a=13;
(2)身高范围在145≤x<155所占的百分比为20%,在155≤x<165范围内的人数最多;
(3)求这些学生身高的平均值;
(4)若该校有800名学生,求身高至少在165cm以上的学生人数.
| 身高(x/cm) | 人数(频数) |
| 145≤x<155 | 10 |
| 155≤x<165 | 25 |
| 165≤x<175 | a |
| 175≤x<185 | 2 |
(1)a=13;
(2)身高范围在145≤x<155所占的百分比为20%,在155≤x<165范围内的人数最多;
(3)求这些学生身高的平均值;
(4)若该校有800名学生,求身高至少在165cm以上的学生人数.
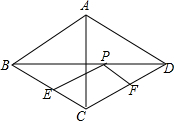 如图,已知菱形ABCD中,对角线AC=12,BD=16,点E、F分别为边BC、CD的中点,点P对角线BD上一动点,则PE+PF的最小值为( )
如图,已知菱形ABCD中,对角线AC=12,BD=16,点E、F分别为边BC、CD的中点,点P对角线BD上一动点,则PE+PF的最小值为( )
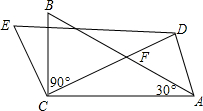 如图所示,在△ABC中,∠ACB=90°,∠A=30°,将△ABC绕点C按逆时针旋转α(0°<α<90°)得△DEC.设CD交AB于点F,当∠ACD=40°或20°时,△ADF为等腰三角形.
如图所示,在△ABC中,∠ACB=90°,∠A=30°,将△ABC绕点C按逆时针旋转α(0°<α<90°)得△DEC.设CD交AB于点F,当∠ACD=40°或20°时,△ADF为等腰三角形.