题目内容
3.观察下列各式,通过分母有理化,把不是最简二次根式的化成最简二次根式:$\frac{1}{\sqrt{2}+1}$=$\frac{1×(\sqrt{2}-1)}{(\sqrt{2}+1)(\sqrt{2}-1)}$=$\frac{\sqrt{2}-1}{2-1}$=$\sqrt{2}$-1,
$\frac{1}{\sqrt{3}+\sqrt{2}}$=$\frac{1×(\sqrt{3}-\sqrt{2})}{(\sqrt{3}+\sqrt{2})(\sqrt{3}-\sqrt{2})}$=$\frac{\sqrt{3}-\sqrt{2}}{3-2}$=$\sqrt{3}$-$\sqrt{2}$,
同理可得:$\frac{1}{2-\sqrt{3}}$=2-$\sqrt{3}$,…
从计算结果中找出规律,并利用这一规律计算
($\frac{1}{\sqrt{2}+1}$+$\frac{1}{\sqrt{3}+\sqrt{2}}$+…+$\frac{1}{\sqrt{2009}+\sqrt{2008}}$)($\sqrt{2009}$+1)的值.
分析 根据已知得出$(\sqrt{2}-1+\sqrt{3}-\sqrt{2}+…+\sqrt{2009}-$$\sqrt{2008})(\sqrt{2009}+1)$$(\sqrt{2009}+1)$,推出$(\sqrt{2009}-1)(\sqrt{2009}+1)$,根据平方差公式求出即可.
解答 解:原式=$(\sqrt{2}-1+\sqrt{3}-\sqrt{2}+…+\sqrt{2009}-$$\sqrt{2008})(\sqrt{2009}+1)$$(\sqrt{2009}+1)$=$(\sqrt{2009}-1)(\sqrt{2009}+1)$=2008.
点评 本题考查了分母有理化的应用,解此题的关键是根据题目的结果找出规律,题目比较好,有一定的难度.

练习册系列答案
相关题目
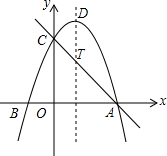 已知抛物线y=ax2+bx+3(a≠0)与x轴交于点A(3、0)和点B(-1,0),与y轴交于点C,抛物线顶点为点D.
已知抛物线y=ax2+bx+3(a≠0)与x轴交于点A(3、0)和点B(-1,0),与y轴交于点C,抛物线顶点为点D.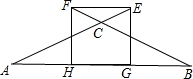 如图,△ABC中,CA=CB,E、F分别在AC、AB的延长线上,且CE=CF,EG⊥AB于G,FH⊥AB于H,连接EF.
如图,△ABC中,CA=CB,E、F分别在AC、AB的延长线上,且CE=CF,EG⊥AB于G,FH⊥AB于H,连接EF.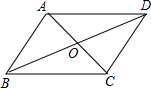 已知如图,?ABCD的对角线AC与BD相交于点O,OA、OB、AB的长分别是3,4,5.求其他各边以及两条对角线的长度.
已知如图,?ABCD的对角线AC与BD相交于点O,OA、OB、AB的长分别是3,4,5.求其他各边以及两条对角线的长度.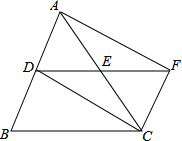 如图,在△ABC中,AC=BC,点D、E分别是边AB、AC的中点,连接DE并延长到点F,使EF=DE,连接AF、CF.求证:四边形ADCF是矩形.
如图,在△ABC中,AC=BC,点D、E分别是边AB、AC的中点,连接DE并延长到点F,使EF=DE,连接AF、CF.求证:四边形ADCF是矩形.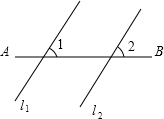 如图,将直线l1沿着AB的方向平移得到直线l2,若∠1=50°,则∠2的度数是50°.
如图,将直线l1沿着AB的方向平移得到直线l2,若∠1=50°,则∠2的度数是50°.