题目内容
13.关于x的多项式乘多项式(x2-3x-2)(ax+1),若结果中不含有x的一次项,求代数式:2a(2a+1)-(2a+1)(2a-1)+1的值.分析 先将式子(x2-3x-2)(ax+1)展开,根据关于x的多项式乘多项式(x2-3x-2)(ax+1)的结果中不含有x的一次项,可以求得a的值,然后再对式子2a(2a+1)-(2a+1)(2a-1)+1进行化简,将a的值代入即可解答本题.
解答 解:(x2-3x-2)(ax+1)
=ax3+x2-3ax2-3x-2ax-2
=ax3+(1-3a)x2-(3+2a)x-2,
∵关于x的多项式乘多项式(x2-3x-2)(ax+1)的结果中不含有x的一次项,
∴3+2a=0,
解得,a=-1.5,
∴2a(2a+1)-(2a+1)(2a-1)+1
=(2a+1)[2a-(2a-1)]+1
=(2a+1)(2a-2a+1)+1
=2a+1+1
=2a+2
=2×(-1.5)+2
=-3+2
=-1,
即2a(2a+1)-(2a+1)(2a-1)+1的值是-1.
点评 本题考查多项式乘以多项式,解题的关键是明确题意,找出所求问题需要的条件.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
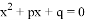 的两根分别为
的两根分别为 ,
,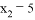 ,那么这个一元二次方程是______.
,那么这个一元二次方程是______. 如图,在平面直角坐标系xOy中,二次函数y=x2-3x的图象与x轴相交于O、A两点.
如图,在平面直角坐标系xOy中,二次函数y=x2-3x的图象与x轴相交于O、A两点.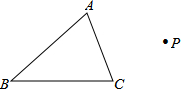 如图,已知△ABC和点O,画出△DEF和△ABC关于点P成中心对称.
如图,已知△ABC和点O,画出△DEF和△ABC关于点P成中心对称.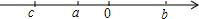 已知实数a,b,c关系是a<0,b>0,c<0,且|c|>|b|>|a|.
已知实数a,b,c关系是a<0,b>0,c<0,且|c|>|b|>|a|.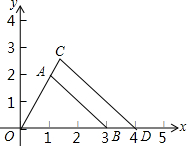 如图,△AOB以O为位似中心,扩大到△COD,各点的坐标分别为A(1,2),B(3,0),D(4,0),求点C的坐标,并求出四边形ABDC的面积.
如图,△AOB以O为位似中心,扩大到△COD,各点的坐标分别为A(1,2),B(3,0),D(4,0),求点C的坐标,并求出四边形ABDC的面积.