题目内容
18.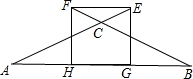 如图,△ABC中,CA=CB,E、F分别在AC、AB的延长线上,且CE=CF,EG⊥AB于G,FH⊥AB于H,连接EF.
如图,△ABC中,CA=CB,E、F分别在AC、AB的延长线上,且CE=CF,EG⊥AB于G,FH⊥AB于H,连接EF.(1)求证:四边形FEGH是矩形;
(2)若∠A=30°,且四边形FEGH是正方形时,求AC:CE的值.
分析 (1根据矩形的判定证明即可;
(2)利用含30°的直角三角形的性质解答即可.
解答 证明:(1)∵CA=CB,CE=CF,
∴∠A=∠B,∠AEF=∠BFE,
∵∠ACF=∠ECB,
∴∠A=∠AEF,
∴EF∥AB,
∵EG⊥AB于G,FH⊥AB于H,
∴EG∥FH,
∴四边形FEGH是平行四边形,
∵EG⊥AB,
∴四边形FEGH是矩形;
(2)设正方形FEGH的边长为1,EG与BF交点为K,
∵∠A=30°,
∴∠B=∠AEF=∠BFE=∠A=30°,
∴AG=$\sqrt{3}$GE=$\sqrt{3}$,EK=$\frac{\sqrt{3}}{3}$EF=$\frac{\sqrt{3}}{3}$,GK=1-$\frac{\sqrt{3}}{3}$,
GB=$\sqrt{3}$GK=$\sqrt{3}(1-\frac{\sqrt{3}}{3})=\sqrt{3}-1$,
∴AB=AG+GB=$2\sqrt{3}$-1,
∵EF∥AB,
∴AC:CE=AB:EF=$2\sqrt{3}$-1.
点评 此题考查了矩形的性质与判定,关键是利用含30°的直角三角形的性质解决问题.

练习册系列答案
相关题目
9.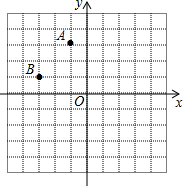 如图,平面直角坐标系中A(-1,3),B(-3,1)
如图,平面直角坐标系中A(-1,3),B(-3,1)
(1)将线段AB平移使A点落在y轴上,B点落在x轴,求线段AB扫过的面积;
(2)若平移后线段AB的中点与(-2,0)重合,求线段AB扫过的面积.
 如图,平面直角坐标系中A(-1,3),B(-3,1)
如图,平面直角坐标系中A(-1,3),B(-3,1)(1)将线段AB平移使A点落在y轴上,B点落在x轴,求线段AB扫过的面积;
(2)若平移后线段AB的中点与(-2,0)重合,求线段AB扫过的面积.
10. 如图,将△ABC沿BC方向平移3cm得到△DEF,若△ABC的周长为20cm,则四边形ABFD的周长为( )
如图,将△ABC沿BC方向平移3cm得到△DEF,若△ABC的周长为20cm,则四边形ABFD的周长为( )
 如图,将△ABC沿BC方向平移3cm得到△DEF,若△ABC的周长为20cm,则四边形ABFD的周长为( )
如图,将△ABC沿BC方向平移3cm得到△DEF,若△ABC的周长为20cm,则四边形ABFD的周长为( )| A. | 20cm | B. | 22cm | C. | 24cm | D. | 26cm |
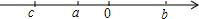 已知实数a,b,c关系是a<0,b>0,c<0,且|c|>|b|>|a|.
已知实数a,b,c关系是a<0,b>0,c<0,且|c|>|b|>|a|.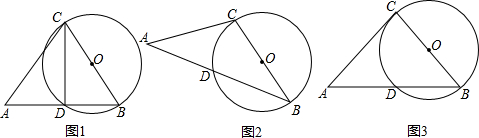
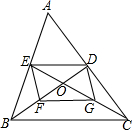 如图,△ABC的中线BD、CE相交于点O,F、G分别是OB、OC的中点.
如图,△ABC的中线BD、CE相交于点O,F、G分别是OB、OC的中点.