题目内容
11.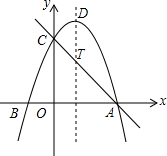 已知抛物线y=ax2+bx+3(a≠0)与x轴交于点A(3、0)和点B(-1,0),与y轴交于点C,抛物线顶点为点D.
已知抛物线y=ax2+bx+3(a≠0)与x轴交于点A(3、0)和点B(-1,0),与y轴交于点C,抛物线顶点为点D.(1)求抛物线的表达式;
(2)直线AC交抛物线对称轴于点T,抛物线上是否存在一点R,使△RDT与△RAT的面积相等?若存在,请求出点R的坐标;若不存在请说明理由.
分析 (1)由A、B两点的坐标,利用待定系数法即可求出抛物线的表达式;
(2)假设存在,设点R的坐标为(n,-n2+2n+3).将抛物线的表达式变形为顶点式,即可得出抛物线对称轴的表达式以及点D的坐标;令x=0,可求出点C的坐标,由A、C两点的坐标结合待定系数法即可求出直线AC的解析式,由两直线相交可求出T点坐标;结合点到直线的距离以及三角形的面积公式即可得出关于n的含绝对值的一元二次方程,解方程即可得出点R的横坐标,代入R点坐标中即可得出结论.
解答 解:(1)将点A(3、0)、点B(-1,0)代入抛物线y=ax2+bx+3中得:
$\left\{\begin{array}{l}{0=9a+3b+3}\\{0=a-b+3}\end{array}\right.$,解得:$\left\{\begin{array}{l}{a=-1}\\{b=2}\end{array}\right.$.
故抛物线的表达式为y=-x2+2x+3.
(2)假设存在,设点R的坐标为(n,-n2+2n+3).
∵抛物线y=-x2+2x+3=-(x-1)2+4,
∴抛物线的对称轴为x=1,点D的坐标为(1,4).
令x=0,则y=3,
即点C的坐标为(0,3).
∴设直线AC的解析式为y=kx+3,
∵点A(3,0)在直线AC上,
∴有0=3k+3=0,解得:k=-1,
∴直线AC的解析式为y=-x+3,即x+y-3=0.
令x=1,则y=-1+3=2,
即点T的坐标为(1,2).
∴DT=4-2=2,AT=$\sqrt{(3-1)^{2}+(0-2)^{2}}$=2$\sqrt{2}$.
点R到直线AC的距离d=$\frac{|n-{n}^{2}+2n+3-3|}{\sqrt{{1}^{2}+{1}^{2}}}$=$\frac{\sqrt{2}}{2}$|3n-n2|;
点R到直线x=1的距离h=|n-1|.
S△RDT=$\frac{1}{2}$DT•h=|n-1|,S△RAT=$\frac{1}{2}$AT•d=|3n-n2|.
∵△RDT与△RAT的面积相等,
∴|n-1|=|3n-n2|,
解得:n1=2+$\sqrt{3}$,n2=2-$\sqrt{3}$,n3=1-$\sqrt{2}$,n4=1+$\sqrt{2}$.
∴点F的坐标为(2+$\sqrt{3}$,-2$\sqrt{3}$),(2-$\sqrt{3}$,2$\sqrt{3}$),(1-$\sqrt{2}$,2)和(1+$\sqrt{2}$,2).
点评 本题考查了待定系数法求函数解析式、点到直线的距离、三角形的面积公式以及解含绝对值的方程,解题的关键是:(1)待定系数法求函解析式;(2)解含绝对值的一元二次方程.本题属于中档题,(1)难度不大;(2)有点难度,难点在于解含绝对值的方程,解题过程中一点要细心仔细.

 阅读快车系列答案
阅读快车系列答案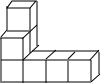 如图,是由相同小正方形组成的立方体图形,它的左视图为( )
如图,是由相同小正方形组成的立方体图形,它的左视图为( )| A. | 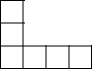 | B. | 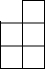 | C. | 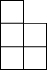 | D. |  |
| A. | (-1,0) | B. | (5,6) | C. | (8,-4) | D. | (1,2) |
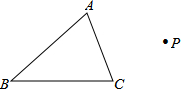 如图,已知△ABC和点O,画出△DEF和△ABC关于点P成中心对称.
如图,已知△ABC和点O,画出△DEF和△ABC关于点P成中心对称. 如图,在?ABCD中,过点C的直线CE⊥AB,垂足为E,若∠EAD=54°,则∠BCE的度数为36°.
如图,在?ABCD中,过点C的直线CE⊥AB,垂足为E,若∠EAD=54°,则∠BCE的度数为36°.