题目内容
12．
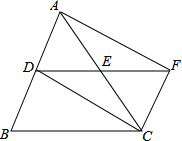如图，在△ABC中，AC=BC，点D、E分别是边AB、AC的中点，连接DE并延长到点F，使EF=DE，连接AF、CF．求证：四边形ADCF是矩形．
分析 先证明四边形ADCF是平行四边形，再证明AC=DF即可．
解答 证明：∵E是AC中点，
∴AE=EC，∵DE=EF，
∴四边形ADCF是平行四边形，
∵AD=DB，AE=EC，
∴DE=$\frac{1}{2}$BC，
∴DF=BC，
∵CA=CB，
∴AC=DF，
∴四边形ADCF是矩形．
点评 本题考查矩形的判定、三角形中位线的性质等知识，记住矩形的判定方法是解题关键，有一个角是直角的平行四边形是矩形，有三个角直角的四边形是矩形，对角线相等的平行四边形是矩形，属于中考常考题型．
练习册系列答案
相关题目
20．将点A（3，2）向下平移2个单位长度后，再向左平移4个单位长度的点为（ ）
| A． | （-1，0） | B． | （5，6） | C． | （8，-4） | D． | （1，2） |
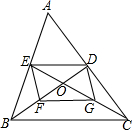如图，△ABC的中线BD、CE相交于点O，F、G分别是OB、OC的中点．
如图，在?ABCD中，AB=$\frac{1}{2}$AD，AB=AE=BF，试探寻CE与DF的位置关系．
如图1，在矩形MNPQ中，动点R从点N出发，沿N→P→Q→M方向运动至点M处停止．设点R运动的路程为x，△MNR的面积为y，如果y关于x的函数图象如图2所示，则y的最大值是（ ）