题目内容
15.化简计算:(1)$(-3)^{0}+(-\frac{1}{2})^{-2}-(-3)^{-1}$
(2)(-2x3)2•(-x2)÷[(-x)2]3.
分析 (1)首先根据零指数幂的运算方法,求出(-3)0的值是多少;然后根据负整数指数幂的运算方法,分别求出${(-\frac{1}{2})}^{-2}$、(-3)-1的值各是多少;最后从左向右依次计算,求出算式的值是多少即可.
(2)有乘方、乘除的混合运算中,要按照先乘方后乘除的顺序运算,其运算顺序和有理数的混合运算顺序相似,据此求出(-2x3)2•(-x2)÷[(-x)2]3的值是多少即可.
解答 解:(1)$(-3)^{0}+(-\frac{1}{2})^{-2}-(-3)^{-1}$
=1+4+$\frac{1}{3}$
=5$+\frac{1}{3}$
=5$\frac{1}{3}$
(2)(-2x3)2•(-x2)÷[(-x)2]3
=4x6•(-x2)÷x6
=-4x8÷x6
=-4x2
点评 (1)此题主要考查了整式的混合运算,要熟练掌握,解答此类问题的关键是要明确:有乘方、乘除的混合运算中,要按照先乘方后乘除的顺序运算,其运算顺序和有理数的混合运算顺序相似.
(2)此题还考查了负整数指数幂的运算,要熟练掌握,解答此题的关键是要明确:①a-p=$\frac{1}{{a}^{p}}$ (a≠0,p为正整数);②计算负整数指数幂时,一定要根据负整数指数幂的意义计算;③当底数是分数时,只要把分子、分母颠倒,负指数就可变为正指数.
(3)此题还考查了零指数幂的运算,要熟练掌握,解答此题的关键是要明确:①a0=1(a≠0);②00≠1.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
10. 如图,将△ABC沿BC方向平移3cm得到△DEF,若△ABC的周长为20cm,则四边形ABFD的周长为( )
如图,将△ABC沿BC方向平移3cm得到△DEF,若△ABC的周长为20cm,则四边形ABFD的周长为( )
 如图,将△ABC沿BC方向平移3cm得到△DEF,若△ABC的周长为20cm,则四边形ABFD的周长为( )
如图,将△ABC沿BC方向平移3cm得到△DEF,若△ABC的周长为20cm,则四边形ABFD的周长为( )| A. | 20cm | B. | 22cm | C. | 24cm | D. | 26cm |
20.将点A(3,2)向下平移2个单位长度后,再向左平移4个单位长度的点为( )
| A. | (-1,0) | B. | (5,6) | C. | (8,-4) | D. | (1,2) |
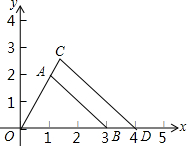 如图,△AOB以O为位似中心,扩大到△COD,各点的坐标分别为A(1,2),B(3,0),D(4,0),求点C的坐标,并求出四边形ABDC的面积.
如图,△AOB以O为位似中心,扩大到△COD,各点的坐标分别为A(1,2),B(3,0),D(4,0),求点C的坐标,并求出四边形ABDC的面积.
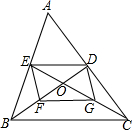 如图,△ABC的中线BD、CE相交于点O,F、G分别是OB、OC的中点.
如图,△ABC的中线BD、CE相交于点O,F、G分别是OB、OC的中点. 如图1,在矩形MNPQ中,动点R从点N出发,沿N→P→Q→M方向运动至点M处停止.设点R运动的路程为x,△MNR的面积为y,如果y关于x的函数图象如图2所示,则y的最大值是( )
如图1,在矩形MNPQ中,动点R从点N出发,沿N→P→Q→M方向运动至点M处停止.设点R运动的路程为x,△MNR的面积为y,如果y关于x的函数图象如图2所示,则y的最大值是( )