题目内容
马航飞机失联后,海空军部队第一时间赴相关海域开展搜寻工作,某舰船在O地修整时发现在它的北偏西60°,距离它40km的A地有一艘搜索船向正东方向航行,经过2小时后,发现此船已到达它东北方向的B处.问搜索船从A处到B处的航速是多少千米/小时(精确到1千米/小时)?(参考数据
≈1.414,
≈1.732,
≈2.236)
| 2 |
| 3 |
| 5 |
考点:解直角三角形的应用-方向角问题
专题:
分析:根据题意先画出图形,再分别解直角三角形AOQ与直角三角形OQB,求出AQ=20
千米,BQ=20千米,然后根据AB=AQ+BQ求出AB的长,则问题可求.
| 3 |
解答: 解:设此船速度为x千米/时,2小时后此船在点B处,作OQ⊥AB于点Q.
解:设此船速度为x千米/时,2小时后此船在点B处,作OQ⊥AB于点Q.
由题意OA=40千米,AB=2x千米.
在直角三角形AOQ中,∠AOQ=60°,
所以OQ=20千米,AQ=20
千米.
在直角三角形OQB中,∠BOQ=45°,
所以,BQ=PQ=20千米,
所以AB=AQ+BQ=20
+20
所以速度=10
+10≈27.
答:搜索船从A处到B处的航速约为27千米/时.
 解:设此船速度为x千米/时,2小时后此船在点B处,作OQ⊥AB于点Q.
解:设此船速度为x千米/时,2小时后此船在点B处,作OQ⊥AB于点Q.由题意OA=40千米,AB=2x千米.
在直角三角形AOQ中,∠AOQ=60°,
所以OQ=20千米,AQ=20
| 3 |
在直角三角形OQB中,∠BOQ=45°,
所以,BQ=PQ=20千米,
所以AB=AQ+BQ=20
| 3 |
所以速度=10
| 3 |
答:搜索船从A处到B处的航速约为27千米/时.
点评:本题考查了解直角三角形的应用-方向角问题,涉及到锐角三角函数、实数的运算、解直角三角形,难度适中.体现了数学与生活的密切联系,同时也进行了实数运算方面的进一步考查,根据题意准确画出图形是解题的关键.

练习册系列答案
相关题目
已知x=3是方程x2+kx+3=0的一个根,则k的值为( )
| A、-2 | B、3 | C、4 | D、-4 |
在平面直角坐标系中,点A的坐标为(2,-3),点A在( )
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |

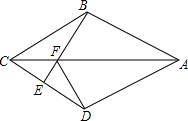 如图,在四边形ABCD中,AB=AD,CB=CD,E是CD上一点,连结BE交AC于点F,连结DF.
如图,在四边形ABCD中,AB=AD,CB=CD,E是CD上一点,连结BE交AC于点F,连结DF.