题目内容
为控制H7N9病毒传播,某地关闭活禽交易,冷冻鸡肉销量上升.某公司在春节期间采购冷冻鸡肉60箱销往城市和乡镇.已知冷冻鸡肉在城市销售平均每箱的利润 y1(百元)与销售数量x(箱)的关系为y1=
和,在乡镇销售平均每箱的利润y2(百元)与销售数量t(箱)的关系为y2=
:
(1)t与x的关系是 ;将y2转换为以x为自变量的函数,则y2= ;
(2)设春节期间售完冷冻鸡肉获得总利润W(百元),当在城市销售量x(箱)的范围是0<x≤20时,求W与x的关系式;(总利润=在城市销售利润+在乡镇销售利润)
(3)经测算,在20<x≤30的范围内,可以获得最大总利润,求这个最大总利润,并求出此时x的值.
|
|
(1)t与x的关系是
(2)设春节期间售完冷冻鸡肉获得总利润W(百元),当在城市销售量x(箱)的范围是0<x≤20时,求W与x的关系式;(总利润=在城市销售利润+在乡镇销售利润)
(3)经测算,在20<x≤30的范围内,可以获得最大总利润,求这个最大总利润,并求出此时x的值.
考点:二次函数的应用
专题:
分析:(1)直接利用采购冷冻鸡肉60箱销往城市和乡镇,表示出t与x的关系即可,进而代入y2求出即可;
(2)利用(1)中所求结合自变量取值范围得出W与x的函数关系式即可;
(3)利用(1)中所求结合自变量取值范围得出W与x的函数关系式,进而利用函数增减性求出函数最值即可.
(2)利用(1)中所求结合自变量取值范围得出W与x的函数关系式即可;
(3)利用(1)中所求结合自变量取值范围得出W与x的函数关系式,进而利用函数增减性求出函数最值即可.
解答:解:(1)∵某公司在春节期间采购冷冻鸡肉60箱销往城市和乡镇,在城市销售数量x(箱),
∴在乡镇销售数量t(箱)的关系为:t=60-x,
∴y2=
.
故答案为:t=60-x,
;
(2)综合y1=
和(1)中 y2,当对应的x范围是0<x≤20 时,
W1=(
x+5)x+(
x+4)(60-x)
=
x2+5x+240;
(3)当20<x≤30 时,
W2=(-
x+75)x+(
x+4)(60-x)
=-
x2+75x+240,
∵x=-
=
>30,
∴W在20<x≤30随x增大而增大,
∴最大值x=30时取得,
∴W最大=832.5(百元).
∴在乡镇销售数量t(箱)的关系为:t=60-x,
∴y2=
|
故答案为:t=60-x,
|
(2)综合y1=
|
W1=(
| 1 |
| 10 |
| 1 |
| 15 |
=
| 1 |
| 30 |
(3)当20<x≤30 时,
W2=(-
| 1 |
| 40 |
| 1 |
| 15 |
=-
| 11 |
| 120 |
∵x=-
| b |
| 2a |
| 450 |
| 11 |
∴W在20<x≤30随x增大而增大,
∴最大值x=30时取得,
∴W最大=832.5(百元).
点评:此题主要考查了二次函数的应用以及二次函数最值求法等知识,得出W与x的函数解析式是解题关键.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案
相关题目
以方程组
的解为坐标的点(x,y)在平面直角坐标系中的位置是( )
|
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
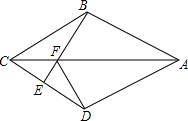 如图,在四边形ABCD中,AB=AD,CB=CD,E是CD上一点,连结BE交AC于点F,连结DF.
如图,在四边形ABCD中,AB=AD,CB=CD,E是CD上一点,连结BE交AC于点F,连结DF.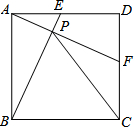 如图,正方形ABCD中,点E从点A出发沿着AD向D运动,(点E不与点A,点D重合)同时点F从点D出发沿着线段DC向C运动,(点F不与点D,点C重合)点E与F点运动速度相同,当点E停止运动时,另一动点F随之停止运动,设BE与AF相交于点P,连接PC请研究:
如图,正方形ABCD中,点E从点A出发沿着AD向D运动,(点E不与点A,点D重合)同时点F从点D出发沿着线段DC向C运动,(点F不与点D,点C重合)点E与F点运动速度相同,当点E停止运动时,另一动点F随之停止运动,设BE与AF相交于点P,连接PC请研究: 如图,在菱形ABCD中,对角线BD=10,E点在BD上,且AE=BE=3,那么这个菱形的边长等于
如图,在菱形ABCD中,对角线BD=10,E点在BD上,且AE=BE=3,那么这个菱形的边长等于