题目内容
6.点P在边长为4的正方形ABCD的边上,AP=5,则△ADP的面积是6或8.分析 根据点P的位置不同分两种情况.①当点P在BC上时,根据正方形的性质利用勾股定理即可求出BP、DP的长度,利用分割图形求面积法即可得出S△ADP的值;②当点P在CD上时,根据正方形的性质利用勾股定理即可求出DP,根据三角形的面积公式即可得出S△ADP的值.综合2种情况,即可得出结论.
解答 解:点P的位置分两种情况(如图所示):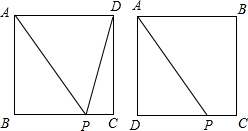
①当点P在BC上时,
∵四边形ABCD为正方形,
∴∠B=90°,
∵AB=4,AP=5,
∴BP=3,CP=1,
∴S△ADP=S正方形ABCD-S△ABP-S△DCP=4×4-$\frac{1}{2}$×3×4-$\frac{1}{2}$×1×4=8;
②当点P在CD上时,
∵∵四边形ABCD为正方形,
∴∠D=90°,
∵AD=4,AP=5,
∴DP=3,
∴S△ADP=$\frac{1}{2}$×3×4=6.
故答案为:6或8.
点评 本题考查了正方形的性质、勾股定理以及三角形的面积公式,解题的关键是分两种情况考虑.本题属于中档题,难度不大,解决该题型题目时,根据点的位置不同分情况考虑是关键.

练习册系列答案
相关题目
15.下列命题中,假命题是( )
| A. | 如果两条直线都与第三条直线平行,那么这两条直线也互相平行 | |
| B. | 在同一平面内,过一点有且只有一条直线与已知直线垂直 | |
| C. | 两条直线被第三条直线所截,同旁内角互补 | |
| D. | 两直线平行,内错角相等 |
3.用两个全等的等边三角形拼成的四边形是( )
| A. | 正方形 | B. | 矩形 | C. | 菱形 | D. | 等腰梯形 |
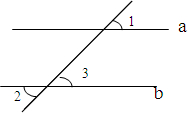 填空:如图,已知∠1=∠2,求证:a∥b
填空:如图,已知∠1=∠2,求证:a∥b 如图,∠C=59°,∠E=50°,AB∥CD,则∠EAB=109°.
如图,∠C=59°,∠E=50°,AB∥CD,则∠EAB=109°. 如图所示,直线AB、CD与直线E、F分别交于E、F两点,已知AB∥CD,∠EFD的平分线FG交AB于点G,∠1=60°,求∠2的度数.
如图所示,直线AB、CD与直线E、F分别交于E、F两点,已知AB∥CD,∠EFD的平分线FG交AB于点G,∠1=60°,求∠2的度数. 如图,点M,N分别在∠AOB的边OA,OB上,且OM=ON.
如图,点M,N分别在∠AOB的边OA,OB上,且OM=ON.