题目内容
17. 若经过一个三角形某一顶点的一条直线可把它分成两个小等腰三角形,那么我们称该三角形为等腰三角形过该顶点的生成三角形.
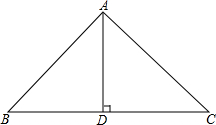
若经过一个三角形某一顶点的一条直线可把它分成两个小等腰三角形,那么我们称该三角形为等腰三角形过该顶点的生成三角形.(1)如图,在等腰Rt△ABC中,AB=AC,∠A=90°,请问△ABC是否是生成三角形?请你说明理由.
(2)若△ABC是等腰三角形过顶点B的生成三角形,∠C是其最小的内角,请探求∠ABC与∠C之间的关系.
分析 (1)作等腰三角形底边上的高是常用的辅助线作法,可把等腰直角三角形分成等腰直角三角形;
(2)根据等腰三角形的性质和外角的性质即可得到结论.
解答 (1)证明:过点A作AD⊥BC,垂足为D.
∵AB=AC,∠BAC=90°,
∴∠B=∠C=45°,∠BAD=∠CAD=$\frac{1}{2}$∠BAC=45°,
∴∠B=∠BAD,∠C=∠CAD.
∴△ABD和△ACD是等腰三角形,
∴△ABC是生成三角形
(2)如图1所示,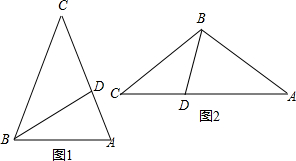 在△ABC中,∵AC=BC,
在△ABC中,∵AC=BC,
∴∠CAB=∠CBA,
由题意得:BD=CD=AB,
∴∠C=∠CBD,∠A=∠ADB,
∵∠ADB=∠C+∠CBD=2∠C=∠A,
∴∠ABC=2∠C,
如图2,由题意得:AB=BC=AD,BD=CD,
∴∠C=∠A=∠CBD,∠ABD=∠ADB,
∵∠ADB=∠C+∠CBD=2∠C,
∴∠ABD=2∠C,
∴∠ABC=3∠C.
点评 本题考查了等腰三角形的性质,等腰直角三角形的性质,外角的性质,熟记等腰三角形的性质是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
8. 如图,将长为14cm的铁丝AB首尾相接围成半径为2cm的扇形,则S扇形=( )
如图,将长为14cm的铁丝AB首尾相接围成半径为2cm的扇形,则S扇形=( )
 如图,将长为14cm的铁丝AB首尾相接围成半径为2cm的扇形,则S扇形=( )
如图,将长为14cm的铁丝AB首尾相接围成半径为2cm的扇形,则S扇形=( )| A. | 12cm2 | B. | 10cm2 | C. | 8cm2 | D. | 6cm2 |
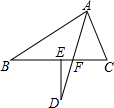 如图,在△ABC中,∠B=30°,∠C=70°,AD平分∠BAC,交BC于F,DE⊥BC于E,则∠D=20°.
如图,在△ABC中,∠B=30°,∠C=70°,AD平分∠BAC,交BC于F,DE⊥BC于E,则∠D=20°.
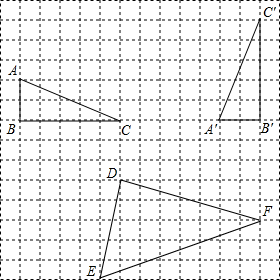 在如图所示的方格图中,每个小正方形的顶点成为“格点”,且每个小正方形的边长均为1个长度单位,以格点为顶点的图形叫做“格点图形”,根据图形解决下列问题:
在如图所示的方格图中,每个小正方形的顶点成为“格点”,且每个小正方形的边长均为1个长度单位,以格点为顶点的图形叫做“格点图形”,根据图形解决下列问题: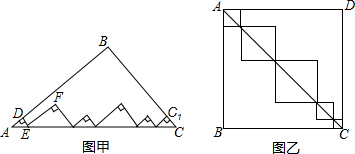
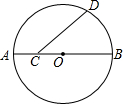 如图,AB为⊙O的直径,C为AB上一点,D为⊙O上一点,且∠DCB=45°,若AC=4,BC=12,求CD的长.
如图,AB为⊙O的直径,C为AB上一点,D为⊙O上一点,且∠DCB=45°,若AC=4,BC=12,求CD的长.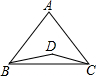 如图,已知AB=AC,BD=CD,∠BDC=150°,∠ABD=40°,求∠BAC的度数.
如图,已知AB=AC,BD=CD,∠BDC=150°,∠ABD=40°,求∠BAC的度数.