题目内容
7．
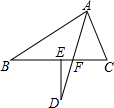如图，在△ABC中，∠B=30°，∠C=70°，AD平分∠BAC，交BC于F，DE⊥BC于E，则∠D=20°．
分析 根据三角形内角和定理易求∠BAC的度数，因为AD平分∠BAC，进而可求出∠CAF的度数，再根据三角形内角和定理可求出∠AFC的度数，由对顶角相等和垂直的性质即可求出∠D的度数．
解答 解：∵∠B=30°，∠C=70°，
∴∠BAC=80°
∵AD平分∠BAC，
∴∠FAC=40°，
∴∠AFC=180°-70°-40°=70°，
∴∠EFD=70°，
∵DE⊥BC于E，
∴∠DEF=90°，
∴∠D=90°70°=20°，
故答案为20．
点评 本题考查了三角形内角和定理：三角形内角和是180°，是基础题，准确识别图形是解题的关键．
练习册系列答案
相关题目
2．不等式$\left\{\begin{array}{l}{x＞2}\\{x＜a}\end{array}\right.$无解，则a的取值范围是（ ）
| A． | a＜2 | B． | a＞2 | C． | a≤2 | D． | a≥2 |
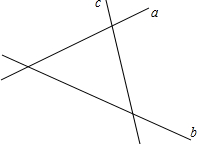如图，有三条公路a，b，c，为了方便司机休息，路政部门确定修建一个休息站P，使它到三条公路的距离相等．（请用尺规作图，保留作图痕迹，不写作法．）
如图，点A，D在反比例函数y=$\frac{8}{x}$（x＞0）的图象上，点A的坐标是（2，4），接AD，过点A作AB⊥AD，交y轴于点B，过点D作DC⊥AD，交x轴于点C，连接BC，四边形ABCD为正方形．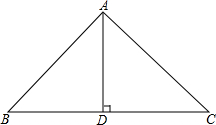
若经过一个三角形某一顶点的一条直线可把它分成两个小等腰三角形，那么我们称该三角形为等腰三角形过该顶点的生成三角形．