题目内容
12.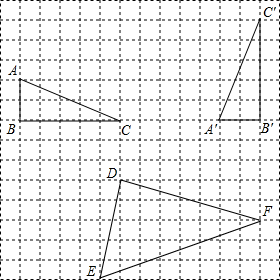 在如图所示的方格图中,每个小正方形的顶点成为“格点”,且每个小正方形的边长均为1个长度单位,以格点为顶点的图形叫做“格点图形”,根据图形解决下列问题:
在如图所示的方格图中,每个小正方形的顶点成为“格点”,且每个小正方形的边长均为1个长度单位,以格点为顶点的图形叫做“格点图形”,根据图形解决下列问题:(1)图中格点△A′B′C′是由格点△ABC通过怎样变换得到的?
(2)如果建立直角坐标系后,点A的坐标为(-6,4),写出图中格点△DEF中各顶点的坐标,并求出过F点的正比例函数解析式.
分析 (1)利用旋转和平移的性质得出△ABC变换的方法;
(2)利用A点坐标得出原点位置进而利用待定系数法求出正比例函数解析式.
解答 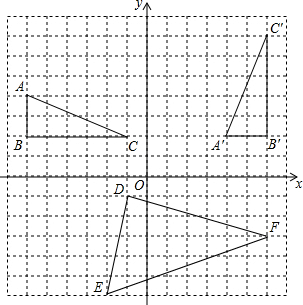 解:(1)格点△A′B′C′是由格点△ABC先绕B点逆时针旋转90°,
解:(1)格点△A′B′C′是由格点△ABC先绕B点逆时针旋转90°,
然后向右平移12个长度单位(或格)得到的.(先平移后旋转也行);
(2)△DEF各顶点的坐标为:D(-1,-1),E(-2,-6),F(6,-4),
设过F点的正比例函数解析式为y=kx,
将F(6,-3)代入上式得,
-3=6k,
解得:k=-$\frac{1}{2}$,
故过A点的正比例函数的解析式为:y=-$\frac{1}{2}$x.
点评 此题主要考查了旋转变换和平移变换以及待定系数法求正比例函数解析式,根据题意得出变换规律是解题关键.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
2.不等式$\left\{\begin{array}{l}{x>2}\\{x<a}\end{array}\right.$无解,则a的取值范围是( )
| A. | a<2 | B. | a>2 | C. | a≤2 | D. | a≥2 |
20.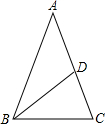 如图,在△ABC中,∠A=36°,AB=AC=2,BD平分∠ABC交AC于点D,则AD等于( )
如图,在△ABC中,∠A=36°,AB=AC=2,BD平分∠ABC交AC于点D,则AD等于( )
 如图,在△ABC中,∠A=36°,AB=AC=2,BD平分∠ABC交AC于点D,则AD等于( )
如图,在△ABC中,∠A=36°,AB=AC=2,BD平分∠ABC交AC于点D,则AD等于( )| A. | $\sqrt{5}$-1 | B. | $\frac{4}{3}$ | C. | 1 | D. | $\frac{\sqrt{5}-1}{2}$ |
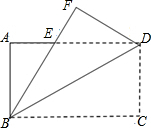 如图所示,把矩形ABCD沿对角线BD折叠,点C落在点F处,若AB=12cm,BC=16cm.
如图所示,把矩形ABCD沿对角线BD折叠,点C落在点F处,若AB=12cm,BC=16cm.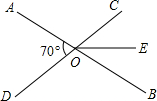 如图,直线AB、CD相交于点O,∠AOD=70°,OE平分∠BOC,求∠DOE的度数.
如图,直线AB、CD相交于点O,∠AOD=70°,OE平分∠BOC,求∠DOE的度数.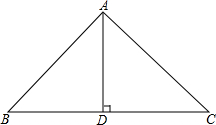 若经过一个三角形某一顶点的一条直线可把它分成两个小等腰三角形,那么我们称该三角形为等腰三角形过该顶点的生成三角形.
若经过一个三角形某一顶点的一条直线可把它分成两个小等腰三角形,那么我们称该三角形为等腰三角形过该顶点的生成三角形. 如图,在Rt△ABC中,∠BAC=90°,AB=AC=2,点D为BC上一点且与B、C不重合.∠ADE=45°,交AC于E.
如图,在Rt△ABC中,∠BAC=90°,AB=AC=2,点D为BC上一点且与B、C不重合.∠ADE=45°,交AC于E.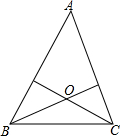 已知点O到△ABC的两边AB,AC所在直线的距离相等,且OB=OC,如图,若点O在△ABC的内部,求证:∠ABO=∠ACO.
已知点O到△ABC的两边AB,AC所在直线的距离相等,且OB=OC,如图,若点O在△ABC的内部,求证:∠ABO=∠ACO.