题目内容
12.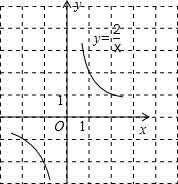 函数y=$\frac{2}{x}$的图象如图所示,在同一直角坐标系内,如果将直线y=-x+1沿y轴向上平移2个单位后,那么所得直线与函数y=$\frac{2}{x}$的图象的交点共有( )个.
函数y=$\frac{2}{x}$的图象如图所示,在同一直角坐标系内,如果将直线y=-x+1沿y轴向上平移2个单位后,那么所得直线与函数y=$\frac{2}{x}$的图象的交点共有( )个.| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
分析 求直线平移后的解析式时要注意平移时k的值不变,只有b发生变化.上下平移时只需让b的值加减即可.
解答 解:y=-x+1的k=-1,b=1,向上平移2个单位后,新直线的k=-1,b=1+2=3.
∴新直线的解析式为:y=-x+3.
有交点,则$\left\{\begin{array}{l}{y=\frac{2}{x}}\\{y=-x+3}\end{array}\right.$,
解得$\left\{\begin{array}{l}{x=1}\\{y=2}\end{array}\right.$或$\left\{\begin{array}{l}{x=2}\\{y=1}\end{array}\right.$.
那么所得直线与函数y=$\frac{2}{x}$的图象的交点共有2个.
故选C.
点评 本题考查了一次函数的平移变换及与反比例函数的交点问题,属于基础题,关键掌握将直线上下平移时k的值不变,只有b发生变化.

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案
相关题目
 如图,在Rt△ABC中,AC=5,BC=12,将Rt△ABC沿AD折叠后,使点C落在AB上的点E处,求CD.
如图,在Rt△ABC中,AC=5,BC=12,将Rt△ABC沿AD折叠后,使点C落在AB上的点E处,求CD.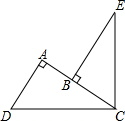 如图,∠DCE=90°,∠DAC=90°,BE⊥AC于点B,且DC=EC,请证明:AB+AD=BE.
如图,∠DCE=90°,∠DAC=90°,BE⊥AC于点B,且DC=EC,请证明:AB+AD=BE.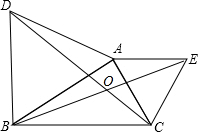 如图,△ABD、△AEC都是等边三角形,BE=4cm,求DC.
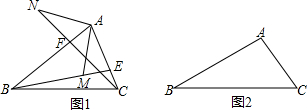
如图,△ABD、△AEC都是等边三角形,BE=4cm,求DC. 如图,四边形ABCD中,AB=DC,∠A=∠D,M、N分别是AD、BC的中点,E、F分别是BM、CM的中点,求证:四边形MENF是菱形.
如图,四边形ABCD中,AB=DC,∠A=∠D,M、N分别是AD、BC的中点,E、F分别是BM、CM的中点,求证:四边形MENF是菱形. 如图,菱形ABCD的边长为4,过点A,C作对角线AC的垂线,分别交CB和AD的延长线于点E,F,AE=3,则四边形AECF的周长为22.
如图,菱形ABCD的边长为4,过点A,C作对角线AC的垂线,分别交CB和AD的延长线于点E,F,AE=3,则四边形AECF的周长为22.
 如图,△ABC∽△AED,AD=5cm,EC=3cm,AC=10cm,则AB=14cm.
如图,△ABC∽△AED,AD=5cm,EC=3cm,AC=10cm,则AB=14cm.